Рассмотрим следующий рисунок:

На нем изображена некоторая функция y = f(x), которая дифференцируема в точке a. Отмечена точка М с координатами (а; f(a)). Через произвольную точку Р(a + ∆x; f(a + ∆x)) графика проведена секущая МР.

Если теперь точку Р сдвигать по графику к точке М, то прямая МР будет поворачиваться вокруг точки М. При этом ∆х будет стремиться к нулю. Отсюда можно сформулировать определение касательной к графику функции.

Касательная к графику функции

Касательная к графику функции есть предельное положение секущей при стремлении приращения аргумента к нулю. Следует понимать, что существование производной функции f в точке х0, означает, что в этой точке графика существует касательная к нему.

При этом угловой коэффициент касательной будет равен производной этой функции в этой точке f’(x0). В этом заключается геометрический смысл производной. Касательная к графику дифференцируемой в точке х0 функции f - это некоторая прямая, проходящая через точку (x0;f(x0)) и имеющая угловой коэффициент f’(x0).

Уравнение касательной

Попытаемся получить уравнение касательной к графику некоторой функции f в точке А(x0; f(x0)). Уравнение прямой с угловым коэффициентом k имеет следующий вид:

Так как у нас угловой коэффициент равен производной f’(x0) , то уравнение примет следующий вид: y = f’(x0) *x + b.

Теперь вычислим значение b. Для этого используем тот факт, что функция проходит через точку А.

f(x0) = f’(x0)*x0 + b, отсюда выражаем b и получим b = f(x0) - f’(x0)*x0.

Подставляем полученное значение в уравнение касательной:

y = f’(x0)*x + b = f’(x0)*x + f(x0) - f’(x0)*x0 = f(x0) + f’(x0)*(x - x0).

y = f(x0) + f’(x0)*(x - x0).

Рассмотрим следующий пример: найти уравнение касательной к графику функции f(x) = x 3 - 2*x 2 + 1 в точке х = 2.

2. f(x0) = f(2) = 2 2 - 2*2 2 + 1 = 1.

3. f’(x) = 3*x 2 - 4*x.

4. f’(x0) = f’(2) = 3*2 2 - 4*2 = 4.

5. Подставим полученные значения в формулу касательной, получим: y = 1 + 4*(x - 2). Раскрыв скобки и приведя подобные слагаемые получим: y = 4*x - 7.

Ответ: y = 4*x - 7.

Общая схема составления уравнения касательной к графику функции y = f(x):

1. Определить х0.

2. Вычислить f(x0).

3. Вычислить f’(x)

Начальный уровень

Уравнение касательной к графику функции. Исчерпывающий гид (2019)

Ты уже знаешь что такое производная? Если нет, сперва прочти тему . Итак, ты говоришь, что знаешь производную. Сейчас проверим. Найди приращение функции при приращении аргумента, равном. Справился? Должно получиться. А теперь найди производную функции в точке. Ответ: . Получилось? Если в каком-нибудь из этих примеров возникли сложности, настоятельно рекомендую вернуться к теме и проштудировать ее еще раз. Знаю, тема очень большая, но иначе нет смысла идти дальше. Рассмотрим график какой-то функции:

Выберем на линии графика некую точку. Пусть ее абсцисса, тогда ордината равна. Затем выберем близкую к точке точку с абсциссой; ее ордината - это:

Проведем прямую через эти точки. Она называется секущей (прямо как в геометрии). Обозначим угол наклона прямой к оси как. Как и в тригонометрии, этот угол отсчитывается от положительного направления оси абсцисс против часовой стрелки. Какие значения может принимать угол? Как ни наклоняй эту прямую, все равно одна половина будет торчать вверх. Поэтому максимально возможный угол - , а минимально возможный - . Значит, . Угол не включается, поскольку положение прямой в этом случае в точности совпадает с, а логичнее выбирать меньший угол. Возьмем на рисунке такую точку, чтобы прямая была параллельна оси абсцисс, а - ординат:

По рисунку видно, что, а. Тогда отношение приращений:

(так как, то - прямоугольный).

Давай теперь уменьшать. Тогда точка будет приближаться к точке. Когда станет бесконечно малым, отношение станет равно производной функции в точке. Что же при этом станет с секущей? Точка будет бесконечно близка к точке, так что их можно будет считать одной и той же точкой. Но прямая, имеющая с кривой только одну общую точку - это ни что иное, как касательная (в данном случае это условие выполняется только на небольшом участке - вблизи точки, но этого достаточно). Говорят, что при этом секущая занимает предельное положение .

Угол наклона секущей к оси назовем. Тогда получится, что производная

то есть производная равна тангенсу угла наклона касательной к графику функции в данной точке.

Поскольку касательная - это прямая, давай теперь вспомним уравнение прямой:

За что отвечает коэффициент? За наклон прямой. Он так и называется: угловой коэффициент . Что это значит? А то, что равен он тангенсу угла между прямой и осью! То есть вот что получается:

Но мы получили это правило, рассматривая возрастающую функцию. А что изменится, если функция будет убывающей? Посмотрим:
Теперь углы и тупые. А приращение функции - отрицательное. Снова рассмотрим: . С другой стороны, . Получаем: , то есть все, как и в прошлый раз. Снова устремим точку к точке, и секущая примет предельное положение, то есть превратится в касательную к графику функции в точке. Итак, сформулируем окончательно полученное правило:
Производная функции в данной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или (что то же самое) угловому коэффициенту этой касательной:

Это и есть геометрический смысл производной. Окей, все это интересно, но зачем оно нам? Вот пример:
На рисунке изображен график функции и касательная к нему в точке с абсциссой. Найдите значение производной функции в точке.
Решение.
Как мы недавно выяснили, значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс: . Значит, для нахождения значения производной нам нужно найти тангенс угла наклона касательной. На рисунке у нас отмечено две точки, лежащие на касательной, координаты которых нам известны. Так давай достроим прямоугольный треугольник, проходящий через эти точки, и найдем тангенс угла наклона касательной!

Угол наклона касательной к оси - это. Найдем тангенс этого угла: . Таким образом, производная функции в точке равна.
Ответ: . Теперь попробуй сам:

Ответы:

Зная геометрический смысл производной , можно очень просто объяснить правило, что производная в точке локального максимума или минимума равна нулю. Действительно, касательная к графику в этих точках «горизонтальна», то есть параллельна оси абсцисс:

А чему равен угол между параллельными прямыми? Конечно, нулю! А тангенс нуля тоже равен нулю. Вот и производная равна нулю:

Более подробно об этом читай в теме «Монотонность функций. Точки экстремума».

А сейчас сосредоточимся на произвольных касательных. Предположим, у нас есть какая-то функция, например, . Мы нарисовали ее график и хотим провести касательную к нему в какой-нибудь точке. Например, в точке. Берем линейку, пристраиваем ее к графику и чертим:

Что мы знаем об этой прямой? Что самое важное нужно знать о прямой на координатной плоскости? Поскольку прямая - это изображение линейной функции, очень удобно было бы знать ее уравнение. То есть коэффициенты и в уравнении

Но ведь мы уже знаем! Это угловой коэффициент касательной, который равен производной функции в этой точке:

В нашем примере будет так:

Теперь остается найти. Это проще простого: ведь - значение при. Графически - это координата пересечения прямой с осью ординат (ведь во всех точках оси):

Проведём (так, что - прямоугольный). Тогда (тому самому углу между касательной и осью абсцисс). Чему равны и? По рисунку явно видно, что, а. Тогда получаем:

Соединяем все полученные формулы в уравнение прямой:

Теперь реши сам:

1. Найди уравнение касательной к функции в точке.
2. Касательная к параболе пересекает ось под углом. Найди уравнение этой касательной.
3. Прямая параллельна касательной к графику функции. Найдите абсциссу точки касания.
4. Прямая параллельна касательной к графику функции. Найдите абсциссу точки касания.

Решения и ответы:

УРАВНЕНИЕ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ. КРАТКОЕ ОПИСАНИЕ И ОСНОВНЫЕ ФОРМУЛЫ

Производная функции в конкретной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или угловому коэффициенту этой касательной:

Уравнение касательной к графику функции в точке:

Алгоритм действий для нахождения уравнения касательной:

Ну вот, тема закончена. Если ты читаешь эти строки, значит ты очень крут.

Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, значит ты попал в эти 5%!

Теперь самое главное.

Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.

Проблема в том, что этого может не хватить…

Для чего?

Для успешной сдачи ЕГЭ, для поступления в институт на бюджет и, САМОЕ ГЛАВНОЕ, для жизни.

Я не буду тебя ни в чем убеждать, просто скажу одну вещь…

Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.

Но и это - не главное.

Главное то, что они БОЛЕЕ СЧАСТЛИВЫ (есть такие исследования). Возможно потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю...

Но, думай сам...

Что нужно, чтобы быть наверняка лучше других на ЕГЭ и быть в конечном итоге… более счастливым?

НАБИТЬ РУКУ, РЕШАЯ ЗАДАЧИ ПО ЭТОЙ ТЕМЕ.

На экзамене у тебя не будут спрашивать теорию.

Тебе нужно будет решать задачи на время .

И, если ты не решал их (МНОГО!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь.

Это как в спорте - нужно много раз повторить, чтобы выиграть наверняка.

Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!

Можно воспользоваться нашими задачами (не обязательно) и мы их, конечно, рекомендуем.

Для того, чтобы набить руку с помощью наших задач нужно помочь продлить жизнь учебнику YouClever, который ты сейчас читаешь.

Как? Есть два варианта:

1. Открой доступ ко всем скрытым задачам в этой статье - 299 руб.
2. Открой доступ ко всем скрытым задачам во всех 99-ти статьях учебника - 999 руб.

Да, у нас в учебнике 99 таких статей и доступ для всех задач и всех скрытых текстов в них можно открыть сразу.

Во втором случае мы подарим тебе тренажер “6000 задач с решениями и ответами, по каждой теме, по всем уровням сложности”. Его точно хватит, чтобы набить руку на решении задач по любой теме.

На самом деле это намного больше, чем просто тренажер - целая программа подготовки. Если понадобится, ты сможешь ею так же воспользоваться БЕСПЛАТНО.

Доступ ко всем текстам и программам предоставляется на ВСЕ время существования сайта.

И в заключение...

Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.

“Понял” и “Умею решать” - это совершенно разные навыки. Тебе нужны оба.

Найди задачи и решай!

Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.

Yandex.RTB R-A-339285-1 Определение 1

Угол наклона прямой y = k x + b называется угол α , который отсчитывается от положительного направления оси о х к прямой y = k x + b в положительном направлении.

На рисунке направление о х обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.

Определение 2

Угловой коэффициент прямой y = k x + b называют числовым коэффициентом k .

Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k = t g α .

• Угол наклона прямой равняется 0 только при параллельности о х и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0 . Значит, вид уравнения будет y = b .
• Если угол наклона прямой y = k x + b острый, тогда выполняются условия 0 < α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α > 0 , причем имеется возрастание графика.
• Если α = π 2 , тогда расположение прямой перпендикулярно о х. Равенство задается при помощи равенства x = c со значением с, являющимся действительным числом.
• Если угол наклона прямой y = k x + b тупой, то соответствует условиям π 2 < α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

Секущей называют прямую, которая проходит через 2 точки функции f (x) . Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.

По рисунку видно, что А В является секущей, а f (x) – черная кривая, α - красная дуга, означающая угол наклона секущей.

Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника А В С можно найти по отношению противолежащего катета к прилежащему.

Определение 4

Получаем формулу для нахождения секущей вида:

k = t g α = B C A C = f (x B) - f x A x B - x A , где абсциссами точек А и В являются значения x A , x B , а f (x A) , f (x B) - это значения функции в этих точках.

Очевидно, что угловой коэффициент секущей определен при помощи равенства k = f (x B) - f (x A) x B - x A или k = f (x A) - f (x B) x A - x B , причем уравнение необходимо записать как y = f (x B) - f (x A) x B - x A · x - x A + f (x A) или
y = f (x A) - f (x B) x A - x B · x - x B + f (x B) .

Секущая делит график визуально на 3 части: слева от точки А, от А до В, справа от В. На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.

По определению видно, что прямая и ее секущая в данном случае совпадают.

Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у = 0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.

Определение 5

Касательная к графику функции f (x) в точке x 0 ; f (x 0) называется прямая, проходящая через заданную точку x 0 ; f (x 0) , с наличием отрезка, который имеет множество значений х, близких к x 0 .

Пример 1

Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y = x + 1 , считается касательной к y = 2 x в точке с координатами (1 ; 2) . Для наглядности, необходимо рассмотреть графики с приближенными к (1 ; 2) значениями. Функция y = 2 x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.

Очевидно, что y = 2 x сливается с прямой у = х + 1 .

Для определения касательной следует рассмотреть поведение касательной А В при бесконечном приближении точки В к точке А. Для наглядности приведем рисунок.

Секущая А В, обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной α x .

Определение 6

Касательной к графику функции y = f (x) в точке А считается предельное положение секущей А В при В стремящейся к А, то есть B → A .

Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.

Перейдем к рассмотрению секущей А В для функции f (x) , где А и В с координатами x 0 , f (x 0) и x 0 + ∆ x , f (x 0 + ∆ x) , а ∆ x обозначаем как приращение аргумента. Теперь функция примет вид ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . Для наглядности приведем в пример рисунок.

Рассмотрим полученный прямоугольный треугольник А В С. Используем определение тангенса для решения, то есть получим отношение ∆ y ∆ x = t g α . Из определения касательной следует, что lim ∆ x → 0 ∆ y ∆ x = t g α x . По правилу производной в точке имеем, что производную f (x) в точке x 0 называют пределом отношений приращения функции к приращению аргумента, где ∆ x → 0 , тогда обозначим как f (x 0) = lim ∆ x → 0 ∆ y ∆ x .

Отсюда следует, что f " (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x , где k x обозначают в качестве углового коэффициента касательной.

То есть получаем, что f ’ (x) может существовать в точке x 0 причем как и касательная к заданному графику функции в точке касания равной x 0 , f 0 (x 0) , где значение углового коэффициента касательной в точке равняется производной в точке x 0 . Тогда получаем, что k x = f " (x 0) .

Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.

Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x 0 при пересечении.

Уравнение касательной к графику функции y = f (x) в точке x 0 , f 0 (x 0) принимает вид y = f " (x 0) · x - x 0 + f (x 0) .

Имеется в виду, что конечным значением производной f " (x 0) можно определить положение касательной, то есть вертикально при условии lim x → x 0 + 0 f " (x) = ∞ и lim x → x 0 - 0 f " (x) = ∞ или отсутствие вовсе при условии lim x → x 0 + 0 f " (x) ≠ lim x → x 0 - 0 f " (x) .

Расположение касательной зависит от значения ее углового коэффициента k x = f " (x 0) . При параллельности к оси о х получаем, что k k = 0 , при параллельности к о у - k x = ∞ , причем вид уравнения касательной x = x 0 возрастает при k x > 0 , убывает при k x < 0 .

Пример 2

Произвести составление уравнения касательной к графику функции y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 в точке с координатами (1 ; 3) с определением угла наклона.

Решение

По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, (1 ; 3) является точкой касания, тогда x 0 = - 1 , f (x 0) = - 3 .

Необходимо найти производную в точке со значением - 1 . Получаем, что

y " = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 " = = e x + 1 " + x 3 3 " - 6 - 3 3 x " - 17 - 3 3 " = e x + 1 + x 2 - 6 - 3 3 y " (x 0) = y " (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3

Значение f ’ (x) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.

Тогда k x = t g α x = y " (x 0) = 3 3

Отсюда следует, что α x = a r c t g 3 3 = π 6

Ответ: уравнение касательной приобретает вид

y = f " (x 0) · x - x 0 + f (x 0) y = 3 3 (x + 1) - 3 y = 3 3 x - 9 - 3 3

Для наглядности приведем пример в графической иллюстрации.

Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.

Пример 3

Выяснить наличие существования касательной к графику заданной функции
y = 3 · x - 1 5 + 1 в точке с координатами (1 ; 1) . Составить уравнение и определить угол наклона.

Решение

По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.

Перейдем к нахождению производной

y " = 3 · x - 1 5 + 1 " = 3 · 1 5 · (x - 1) 1 5 - 1 = 3 5 · 1 (x - 1) 4 5

Если x 0 = 1 , тогда f ’ (x) не определена, но пределы записываются как lim x → 1 + 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (+ 0) 4 5 = 3 5 · 1 + 0 = + ∞ и lim x → 1 - 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞ , что означает существование вертикальной касательной в точке (1 ; 1) .

Ответ: уравнение примет вид х = 1 , где угол наклона будет равен π 2 .

Для наглядности изобразим графически.

Пример 4

Найти точки графика функции y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2 , где

1. Касательная не существует;
2. Касательная располагается параллельно о х;
3. Касательная параллельна прямой y = 8 5 x + 4 .

Решение

Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x ∈ - ∞ ; 2 и [ - 2 ; + ∞) . Получаем, что

y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; + ∞)

Необходимо продифференцировать функцию. Имеем, что

y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 " , x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; + ∞)

Когда х = - 2 , тогда производная не существует, потому что односторонние пределы не равны в этой точке:

lim x → - 2 - 0 y " (x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y " (x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3

Вычисляем значение функции в точке х = - 2 , где получаем, что

1. y (- 2) = 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 = - 2 , то есть касательная в точке (- 2 ; - 2) не будет существовать.
2. Касательная параллельна о х, когда угловой коэффициент равняется нулю. Тогда k x = t g α x = f " (x 0) . То есть необходимо найти значения таких х, когда производная функции обращает ее в ноль. То есть значения f ’ (x) и будут являться точками касания, где касательная является параллельной о х.

Когда x ∈ - ∞ ; - 2 , тогда - 1 5 (x 2 + 12 x + 35) = 0 , а при x ∈ (- 2 ; + ∞) получаем 1 5 (x 2 - 4 x + 3) = 0 .

1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 · 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 · 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; + ∞

Вычисляем соответствующие значения функции

y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 · 1 2 - 16 5 · 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 · 3 2 - 16 5 · 3 - 26 5 + 3 3 + 2 = 4 3

Отсюда - 5 ; 8 5 , - 4 ; 4 3 , 1 ; 8 5 , 3 ; 4 3 считаются искомыми точками графика функции.

Рассмотрим графическое изображение решения.

Черная линия – график функции, красные точки – точки касания.

1. Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 8 5 . Для этого нужно решить уравнение вида y " (x) = 8 5 . Тогда, если x ∈ - ∞ ; - 2 , получаем, что - 1 5 (x 2 + 12 x + 35) = 8 5 , а если x ∈ (- 2 ; + ∞) , тогда 1 5 (x 2 - 4 x + 3) = 8 5 .

Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 · 43 = - 28 < 0

Другое уравнение имеет два действительных корня, тогда

1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 · (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; + ∞

Перейдем к нахождению значений функции. Получаем, что

y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 · 5 2 - 16 5 · 5 - 26 5 + 3 5 + 2 = 8 3

Точки со значениями - 1 ; 4 15 , 5 ; 8 3 являются точками, в которых касательные параллельны прямой y = 8 5 x + 4 .

Ответ: черная линия – график функции, красная линия – график y = 8 5 x + 4 , синяя линия – касательные в точках - 1 ; 4 15 , 5 ; 8 3 .

Возможно существование бесконечного количества касательных для заданных функций.

Пример 5

Написать уравнения всех имеющихся касательных функции y = 3 cos 3 2 x - π 4 - 1 3 , которые располагаются перпендикулярно прямой y = - 2 x + 1 2 .

Решение

Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется - 1 , то есть записывается как k x · k ⊥ = - 1 . Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k ⊥ = - 2 , тогда k x = - 1 k ⊥ = - 1 - 2 = 1 2 .

Теперь необходимо найти координаты точек касания. Нужно найти х, после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x 0 получаем, что k x = y " (x 0) . Из данного равенства найдем значения х для точек касания.

Получаем, что

y " (x 0) = 3 cos 3 2 x 0 - π 4 - 1 3 " = 3 · - sin 3 2 x 0 - π 4 · 3 2 x 0 - π 4 " = = - 3 · sin 3 2 x 0 - π 4 · 3 2 = - 9 2 · sin 3 2 x 0 - π 4 ⇒ k x = y " (x 0) ⇔ - 9 2 · sin 3 2 x 0 - π 4 = 1 2 ⇒ sin 3 2 x 0 - π 4 = - 1 9

Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.

3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk или 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk

3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk или 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 - a r c sin 1 9 + 2 πk или x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z - множество целых чисел.

Найдены х точек касания. Теперь необходимо перейти к поиску значений у:

y 0 = 3 cos 3 2 x 0 - π 4 - 1 3

y 0 = 3 · 1 - sin 2 3 2 x 0 - π 4 - 1 3 или y 0 = 3 · - 1 - sin 2 3 2 x 0 - π 4 - 1 3

y 0 = 3 · 1 - - 1 9 2 - 1 3 или y 0 = 3 · - 1 - - 1 9 2 - 1 3

y 0 = 4 5 - 1 3 или y 0 = - 4 5 + 1 3

Отсюда получаем, что 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; - 4 5 + 1 3 являются точками касания.

Ответ: необходимы уравнения запишутся как

y = 1 2 x - 2 3 π 4 - a r c sin 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + a r c sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z

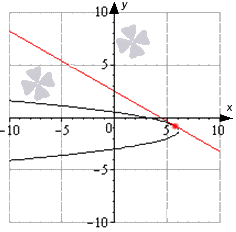
Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.

Рисунок показывает, что расположение функции идет на промежутке [ - 10 ; 10 ] , где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y = - 2 x + 1 2 . Красные точки – это точки касания.

Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.

Касательная к окружности

Для задания окружности с центром в точке x c e n t e r ; y c e n t e r и радиусом R применяется формула x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 .

Данное равенство может быть записано как объединение двух функций:

y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r

Первая функция располагается вверху, а вторая внизу, как показано на рисунке.

Для составления уравнения окружности в точке x 0 ; y 0 , которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y = R 2 - x - x c e n t e r 2 + y c e n t e r или y = - R 2 - x - x c e n t e r 2 + y c e n t e r в указанной точке.

Когда в точках x c e n t e r ; y c e n t e r + R и x c e n t e r ; y c e n t e r - R касательные могут быть заданы уравнениями y = y c e n t e r + R и y = y c e n t e r - R , а в точках x c e n t e r + R ; y c e n t e r и
x c e n t e r - R ; y c e n t e r будут являться параллельными о у, тогда получим уравнения вида x = x c e n t e r + R и x = x c e n t e r - R .

Касательная к эллипсу

Когда эллипс имеет центр в точке x c e n t e r ; y c e n t e r с полуосями a и b , тогда он может быть задан при помощи уравнения x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1 .

Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что

y = b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r

Если касательные располагаются на вершинах эллипса, тогда они параллельны о х или о у. Ниже для наглядности рассмотрим рисунок.

Пример 6

Написать уравнение касательной к эллипсу x - 3 2 4 + y - 5 2 25 = 1 в точках со значениями x равного х = 2 .

Решение

Необходимо найти точки касания, которые соответствуют значению х = 2 . Производим подстановку в имеющееся уравнение эллипса и получаем, что

x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 · 25 ⇒ y = ± 5 3 2 + 5

Тогда 2 ; 5 3 2 + 5 и 2 ; - 5 3 2 + 5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.

Перейдем к нахождению и разрешению уравнения эллипса относительно y . Получим, что

x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 · 1 - x - 3 2 4 y - 5 = ± 5 · 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2

Очевидно, что верхний полуэллипс задается с помощью функции вида y = 5 + 5 2 4 - x - 3 2 , а нижний y = 5 - 5 2 4 - x - 3 2 .

Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2 ; 5 3 2 + 5 будет иметь вид

y " = 5 + 5 2 4 - x - 3 2 " = 5 2 · 1 2 4 - (x - 3) 2 · 4 - (x - 3) 2 " = = - 5 2 · x - 3 4 - (x - 3) 2 ⇒ y " (x 0) = y " (2) = - 5 2 · 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y " (x 0) · x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5

Получаем, что уравнение второй касательной со значением в точке
2 ; - 5 3 2 + 5 принимает вид

y " = 5 - 5 2 4 - (x - 3) 2 " = - 5 2 · 1 2 4 - (x - 3) 2 · 4 - (x - 3) 2 " = = 5 2 · x - 3 4 - (x - 3) 2 ⇒ y " (x 0) = y " (2) = 5 2 · 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y " (x 0) · x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5

Графически касательные обозначаются так:

Касательная к гиперболе

Когда гипербола имеет центр в точке x c e n t e r ; y c e n t e r и вершины x c e n t e r + α ; y c e n t e r и x c e n t e r - α ; y c e n t e r , имеет место задание неравенства x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1 , если с вершинами x c e n t e r ; y c e n t e r + b и x c e n t e r ; y c e n t e r - b , тогда задается при помощи неравенства x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 .

Гипербола может быть представлена в виде двух объединенных функций вида

y = b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r или y = b a · (x - x c e n t e r) 2 + a 2 + y c e n t e r y = - b a · (x - x c e n t e r) 2 + a 2 + y c e n t e r

В первом случае имеем, что касательные параллельны о у, а во втором параллельны о х.

Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.

Пример 7

Составить уравнение касательной к гиперболе x - 3 2 4 - y + 3 2 9 = 1 в точке 7 ; - 3 3 - 3 .

Решение

Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что

x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 · x - 3 2 4 - 1 ⇒ y + 3 = 3 2 · x - 3 2 - 4 и л и y + 3 = - 3 2 · x - 3 2 - 4 ⇒ y = 3 2 · x - 3 2 - 4 - 3 y = - 3 2 · x - 3 2 - 4 - 3

Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7 ; - 3 3 - 3 .

Очевидно, что для проверки первой функции необходимо y (7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3 , тогда точка графику не принадлежит, так как равенство не выполняется.

Для второй функции имеем, что y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3 , значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.

Получаем, что

y " = - 3 2 · (x - 3) 2 - 4 - 3 " = - 3 2 · x - 3 (x - 3) 2 - 4 ⇒ k x = y " (x 0) = - 3 2 · x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 · 7 - 3 7 - 3 2 - 4 = - 3

Ответ: уравнение касательной можно представить как

y = - 3 · x - 7 - 3 3 - 3 = - 3 · x + 4 3 - 3

Наглядно изображается так:

Касательная к параболе

Чтобы составить уравнение касательной к параболе y = a x 2 + b x + c в точке x 0 , y (x 0) , необходимо использовать стандартный алгоритм, тогда уравнение примет вид y = y " (x 0) · x - x 0 + y (x 0) . Такая касательная в вершине параллельна о х.

Следует задать параболу x = a y 2 + b y + c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у. Получаем, что

x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a

Графически изобразим как:

Для выяснения принадлежности точки x 0 , y (x 0) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна о у относительно параболы.

Пример 8

Написать уравнение касательной к графику x - 2 y 2 - 5 y + 3 , когда имеем угол наклона касательной 150 ° .

Решение

Начинаем решение с представления параболы в качестве двух функций. Получим, что

2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 · (- 2) · (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4

Значение углового коэффициента равняется значению производной в точке x 0 этой функции и равняется тангенсу угла наклона.

Получаем:

k x = y " (x 0) = t g α x = t g 150 ° = - 1 3

Отсюда определим значение х для точек касания.

Первая функция запишется как

y " = 5 + 49 - 8 x - 4 " = 1 49 - 8 x ⇒ y " (x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3

Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150 ° для такой функции не существует.

Вторая функция запишется как

y " = 5 - 49 - 8 x - 4 " = - 1 49 - 8 x ⇒ y " (x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 · 23 4 - 4 = - 5 + 3 4

Имеем, что точки касания - 23 4 ; - 5 + 3 4 .

Ответ: уравнение касательной принимает вид

y = - 1 3 · x - 23 4 + - 5 + 3 4

Графически изобразим это таким образом:

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Касательная – это прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка (рис.1).

Другое определение : это предельное положение секущей при Δx →0.

Пояснение : Возьмем прямую, пересекающую кривую в двух точках: А и b (см.рисунок). Это секущая. Будем поворачивать ее по часовой стрелке до тех пор, пока она не обретет только одну общую точку с кривой. Так мы получим касательную.

Строгое определение касательной:

Касательная к графику функции f , дифференцируемой в точке x о , - это прямая, проходящая через точку (x о ; f (x о )) и имеющая угловой коэффициент f ′(x о ).

Угловой коэффициент имеет прямая вида y = kx + b . Коэффициент k и является угловым коэффициентом этой прямой.

Угловой коэффициент равен тангенсу острого угла, образуемого этой прямой с осью абсцисс:

Здесь угол α – это угол между прямой y = kx + b и положительным (то есть против часовой стрелки) направлением оси абсцисс. Он называется углом наклона прямой (рис.1 и 2).

Если угол наклона прямой y = kx + b острый, то угловой коэффициент является положительным числом. График возрастает (рис.1).

Если угол наклона прямой y = kx + b тупой, то угловой коэффициент является отрицательным числом. График убывает (рис.2).

Если прямая параллельна оси абсцисс, то угол наклона прямой равен нулю. В этом случае угловой коэффициент прямой тоже равен нулю (так как тангенс нуля есть ноль). Уравнение прямой будет иметь вид y = b (рис.3).

Если угол наклона прямой равен 90º (π/2), то есть она перпендикулярна оси абсцисс, то прямая задается равенством x = c , где c – некоторое действительное число (рис.4).

Уравнение касательной к графику функции y = f (x ) в точке x о :

Пример : Найдем уравнение касательной к графику функции f (x ) = x 3 – 2x 2 + 1 в точке с абсциссой 2.

Решение .

Следуем алгоритму.

1) Точка касания x о равна 2. Вычислим f (x о ):

f (x о ) = f (2) = 2 3 – 2 ∙ 2 2 + 1 = 8 – 8 + 1 = 1

2) Находим f ′(x ). Для этого применяем формулы дифференцирования, изложенные в предыдущем разделе. Согласно этим формулам, х 2 = 2х , а х 3 = 3х 2 . Значит:

f ′(x ) = 3х 2 – 2 ∙ 2х = 3х 2 – 4х .

Теперь, используя полученное значение f ′(x ), вычислим f ′(x о ):

f ′(x о ) = f ′(2) = 3 ∙ 2 2 – 4 ∙ 2 = 12 – 8 = 4.

3) Итак, у нас есть все необходимые данные: x о = 2, f (x о ) = 1, f ′(x о ) = 4. Подставляем эти числа в уравнение касательной и находим окончательное решение:

у = f (x о ) + f ′(x о ) (x – x о ) = 1 + 4 ∙ (х – 2) = 1 + 4х – 8 = –7 + 4х = 4х – 7.

Ответ : у = 4х – 7.