Logaritmické nerovnosti
V predchádzajúcich lekciách sme sa zoznámili s logaritmickými rovnicami a teraz vieme, čo sú a ako ich riešiť. Dnešná lekcia bude venovaná štúdiu logaritmických nerovností. Aké sú tieto nerovnosti a aký je rozdiel medzi riešením logaritmickej rovnice a nerovnicou?
Logaritmické nerovnosti- sú to nerovnosti, ktoré majú premennú pod znamienkom logaritmu alebo na jeho báze.
Alebo môžeme tiež povedať, že logaritmická nerovnosť je nerovnosť, v ktorej sa jej neznáma hodnota, ako v logaritmickej rovnici, objaví pod znamienkom logaritmu.
Najjednoduchšie logaritmické nerovnosti majú nasledujúci tvar:
kde f(x) a g(x) sú nejaké výrazy, ktoré závisia od x.
Pozrime sa na to pomocou tohto príkladu: f(x)=1+2x+x2, g(x)=3x−1.
Riešenie logaritmických nerovností
Pred riešením logaritmických nerovností stojí za zmienku, že po vyriešení sú podobné exponenciálnym nerovnostiam, konkrétne:
Po prvé, keď prechádzame od logaritmov k výrazom pod logaritmickým znamienkom, musíme tiež porovnať základ logaritmu s jedným;
Po druhé, pri riešení logaritmickej nerovnosti pomocou zmeny premenných musíme riešiť nerovnosti vzhľadom na zmenu, kým nedostaneme najjednoduchšiu nerovnosť.
Ale vy a ja sme zvažovali podobné aspekty riešenia logaritmických nerovností. Teraz sa pozrime na pomerne významný rozdiel. Vy a ja vieme, že logaritmická funkcia má obmedzenú oblasť definície, preto pri prechode od logaritmov k výrazom pod logaritmickým znakom musíme vziať do úvahy rozsah povolených hodnôt (ADV).
To znamená, že by sa malo vziať do úvahy, že pri riešení logaritmickej rovnice môžeme vy a ja najprv nájsť korene rovnice a potom toto riešenie skontrolovať. Riešenie logaritmickej nerovnosti však nebude fungovať týmto spôsobom, pretože pri prechode od logaritmov k výrazom pod logaritmickým znamienkom bude potrebné zapísať ODZ nerovnosti.
Okrem toho je potrebné pripomenúť, že teória nerovností pozostáva z reálnych čísel, čo sú kladné a záporné čísla, ako aj číslo 0.
Napríklad, keď je číslo „a“ kladné, musíte použiť nasledujúci zápis: a >0. V tomto prípade bude súčet aj súčin týchto čísel kladné.
Hlavným princípom riešenia nerovnosti je nahradiť ju jednoduchšou nerovnicou, ale hlavné je, že je ekvivalentná danej. Ďalej sme tiež získali nerovnosť a opäť sme ju nahradili nerovnosťou, ktorá má jednoduchší tvar atď.
Pri riešení nerovností s premennou je potrebné nájsť všetky jej riešenia. Ak majú dve nerovnosti rovnakú premennú x, potom sú takéto nerovnosti ekvivalentné za predpokladu, že sa ich riešenia zhodujú.
Pri vykonávaní úloh na riešenie logaritmických nerovností si musíte pamätať, že keď a > 1, potom sa logaritmická funkcia zvýši a keď 0< a < 1, то такая функция имеет свойство убывать. Эти свойства вам будут необходимы при решении логарифмических неравенств, поэтому вы их должны хорошо знать и помнить.
Metódy riešenia logaritmických nerovností
Teraz sa pozrime na niektoré metódy, ktoré sa používajú pri riešení logaritmických nerovností. Pre lepšie pochopenie a asimiláciu sa ich pokúsime pochopiť na konkrétnych príkladoch.
Všetci vieme, že najjednoduchšia logaritmická nerovnosť má nasledujúci tvar:
V tejto nerovnosti je V – jedným z nasledujúcich znakov nerovnosti:<,>, ≤ alebo ≥.
Keď je základ daného logaritmu väčší ako jedna (a>1), pri prechode z logaritmov na výrazy pod znamienkom logaritmu sa v tejto verzii znamienko nerovnosti zachová a nerovnosť bude mať nasledujúci tvar:
ktorý je ekvivalentný tomuto systému:

V prípade, že základ logaritmu je väčší ako nula a menší ako jedna (0 Toto je ekvivalentné tomuto systému: Pozrime sa na ďalšie príklady riešenia najjednoduchších logaritmických nerovností znázornených na obrázku nižšie: Cvičenie. Pokúsme sa vyriešiť túto nerovnosť: Riešenie rozsahu prijateľných hodnôt. Teraz skúsme vynásobiť jeho pravú stranu: Pozrime sa, čo môžeme vymyslieť: Teraz prejdime ku konverzii sublogaritmických výrazov. Vzhľadom k tomu, že základ logaritmu je 0< 1/4 <1, то от сюда следует, что знак неравенства изменится на противоположный: 3x - 8 > 16; A z toho vyplýva, že interval, ktorý sme získali úplne patrí do ODZ a je riešením takejto nerovnosti. Tu je odpoveď, ktorú sme dostali: Teraz sa pokúsme analyzovať, čo potrebujeme na úspešné vyriešenie logaritmických nerovností? Najprv sústreďte všetku svoju pozornosť a snažte sa nerobiť chyby pri vykonávaní transformácií, ktoré sú dané v tejto nerovnosti. Treba tiež pamätať na to, že pri riešení takýchto nerovností je potrebné vyhnúť sa rozširovaniu a zmršťovaniu nerovností, čo môže viesť k strate alebo získaniu cudzích riešení. Po druhé, pri riešení logaritmických nerovností sa musíte naučiť myslieť logicky a pochopiť rozdiel medzi pojmami, ako je systém nerovností a množina nerovností, aby ste mohli ľahko vyberať riešenia nerovnosti, pričom sa riadite jej DL. Po tretie, na úspešné vyriešenie takýchto nerovností musí každý z vás dokonale poznať všetky vlastnosti elementárnych funkcií a jasne pochopiť ich význam. Medzi takéto funkcie patria nielen logaritmické, ale aj racionálne, mocenské, trigonometrické atď., jedným slovom, všetky tie, ktoré ste študovali počas školskej algebry. Ako vidíte, po preštudovaní témy logaritmických nerovností nie je pri riešení týchto nerovností nič ťažké, za predpokladu, že ste opatrní a vytrvalí pri dosahovaní svojich cieľov. Aby ste sa vyhli akýmkoľvek problémom pri riešení nerovností, musíte sa čo najviac precvičiť, riešiť rôzne úlohy a zároveň si zapamätať základné metódy riešenia takýchto nerovností a ich sústavy. Ak sa vám nepodarí vyriešiť logaritmické nerovnosti, mali by ste svoje chyby dôkladne analyzovať, aby ste sa k nim v budúcnosti nevrátili. Ak chcete lepšie porozumieť téme a konsolidovať preberaný materiál, vyriešte nasledujúce nerovnosti: Ciele lekcie: Didaktické: Vzdelávacie: rozvíjať pamäť, pozornosť, logické myslenie, porovnávacie schopnosti, vedieť zovšeobecňovať a vyvodzovať závery Vzdelávacie: kultivovať presnosť, zodpovednosť za vykonávanú úlohu a vzájomnú pomoc. Vyučovacie metódy:
verbálne ,
vizuálny ,
praktické ,
čiastočné vyhľadávanie ,
samospráva ,
ovládanie. Formy organizácie kognitívnej činnosti študentov:
čelný ,
individuálne ,
pracovať v pároch. Vybavenie:
súbor testových úloh, referenčné poznámky, prázdne hárky na riešenia. Typ lekcie: učenie sa nového materiálu. Počas vyučovania 1. Organizačný moment. Oznamuje sa téma a ciele hodiny, plán hodiny: každý študent dostane hodnotiaci hárok, ktorý študent počas hodiny vypĺňa; pre každú dvojicu žiakov - tlačené materiály s úlohami musia byť vyplnené vo dvojiciach; prázdne hárky s roztokom; podporné listy: definícia logaritmu; graf logaritmickej funkcie, jej vlastnosti; vlastnosti logaritmov; Algoritmus na riešenie logaritmických nerovností. Všetky rozhodnutia po sebahodnotení sa predkladajú vyučujúcemu. Výsledkový list študenta 2. Aktualizácia vedomostí. Pokyny učiteľa. Spomeňte si na definíciu logaritmu, graf logaritmickej funkcie a jej vlastnosti. Na tento účel si prečítajte text na s. 88–90, 98–101 učebnice „Algebra a začiatky analýzy 10–11“, ktorú vydali Sh.A Alimov, Yu.M Kolyagin a iní. Študenti dostanú hárky, na ktorých sú napísané: definícia logaritmu; ukazuje graf logaritmickej funkcie a jej vlastnosti; vlastnosti logaritmov; algoritmus na riešenie logaritmických nerovností, príklad riešenia logaritmickej nerovnosti, ktorá sa redukuje na kvadratickú. 3. Štúdium nového materiálu. Riešenie logaritmických nerovností je založené na monotónnosti logaritmickej funkcie. Algoritmus na riešenie logaritmických nerovností: A) Nájdite definičný obor nerovnice (sublogaritmický výraz je väčší ako nula). Učebný prvok #1. Cieľ: konsolidovať riešenie najjednoduchších logaritmických nerovností Forma organizácie poznávacej činnosti žiakov: samostatná práca. Úlohy na samostatnú prácu na 10 minút. Pre každú nerovnosť existuje niekoľko možných odpovedí, musíte vybrať správnu a skontrolovať ju pomocou kľúča. Učebný prvok č. 2. Cieľ: konsolidovať riešenie logaritmických nerovností pomocou vlastností logaritmov. Pokyny učiteľa. Pamätajte na základné vlastnosti logaritmov. K tomu si prečítajte text učebnice na s. 92, 103–104. Úlohy na samostatnú prácu na 10 minút. KĽÚČ: 2113, maximálny počet bodov – 8 bodov. Učebný prvok č. 3. Účel: študovať riešenie logaritmických nerovností metódou redukcie na kvadratickú. Inštrukcie učiteľa: metóda redukcie nerovnosti na kvadratickú je transformovať nerovnosť do takého tvaru, že určitá logaritmická funkcia je označená novou premennou, čím sa získa kvadratická nerovnosť vzhľadom na túto premennú. Využime intervalovú metódu. Prešli ste prvou úrovňou zvládnutia materiálu. Teraz si budete musieť nezávisle zvoliť metódu riešenia logaritmických rovníc s využitím všetkých svojich vedomostí a schopností. Učebný prvok č. 4. Cieľ: konsolidovať riešenie logaritmických nerovností nezávislým výberom metódy racionálneho riešenia. Úlohy na samostatnú prácu na 10 minút Učebný prvok č. 5. Pokyny učiteľa. Výborne! Zvládli ste riešenie rovníc druhého stupňa zložitosti. Cieľom vašej ďalšej práce je uplatniť svoje vedomosti a zručnosti v zložitejších a neštandardných situáciách. Úlohy na samostatné riešenie: Pokyny učiteľa. Je skvelé, ak ste splnili celú úlohu. Výborne! Známka za celú hodinu závisí od počtu bodov získaných za všetky vzdelávacie prvky: Hodnotiace papiere odovzdajte učiteľovi. 5. Domáca úloha: ak ste dosiahli maximálne 15 bodov, pracujte na svojich chybách (riešenia získate od učiteľa), ak ste dosiahli viac ako 15 bodov, dokončite kreatívnu úlohu na tému „Logaritmické nerovnosti“. Myslíte si, že do Jednotnej štátnej skúšky je ešte čas a stihnete sa pripraviť? Možno je to tak. V každom prípade však platí, že čím skôr študent začne s prípravou, tým úspešnejšie zloží skúšky. Dnes sme sa rozhodli venovať článok logaritmickým nerovnostiam. Toto je jedna z úloh, ktorá znamená možnosť získať kredit navyše. Už viete, čo je logaritmus? Naozaj dúfame. Ale aj keď na túto otázku nemáte odpoveď, nie je to problém. Pochopenie toho, čo je logaritmus, je veľmi jednoduché. Prečo 4? Ak chcete získať 81, musíte zvýšiť číslo 3 na túto mocninu. Keď pochopíte princíp, môžete pristúpiť k zložitejším výpočtom. Pred pár rokmi ste prešli nerovnosťami. A odvtedy sa s nimi v matematike neustále stretávate. Ak máte problémy s riešením nerovností, pozrite si príslušnú sekciu. Najjednoduchšia logaritmická nerovnosť. Najjednoduchšie logaritmické nerovnosti nie sú obmedzené na tento príklad, existujú tri ďalšie, len s rôznymi znamienkami. Prečo je to potrebné? Aby sme lepšie pochopili, ako riešiť nerovnosti pomocou logaritmov. Teraz uveďme použiteľnejší príklad, stále celkom jednoduchý, zložité logaritmické nerovnosti si necháme na neskôr. Ako to vyriešiť? Všetko to začína ODZ. Stojí za to vedieť o tom viac, ak chcete vždy ľahko vyriešiť akúkoľvek nerovnosť. Skratka znamená rozsah prijateľných hodnôt. Táto formulácia sa často objavuje v úlohách jednotnej štátnej skúšky. ODZ sa vám bude hodiť nielen v prípade logaritmických nerovností. Pozrite sa znova na vyššie uvedený príklad. Na základe toho zvážime ODZ, aby ste pochopili princíp a riešenie logaritmických nerovností nevyvoláva otázky. Z definície logaritmu vyplýva, že 2x+4 musí byť väčšie ako nula. V našom prípade to znamená nasledovné. Toto číslo musí byť podľa definície kladné. Vyriešte vyššie uvedenú nerovnosť. Dá sa to urobiť aj ústne, tu je jasné, že X nemôže byť menšie ako 2. Riešením nerovnosti bude definovanie rozsahu prijateľných hodnôt. Samotné logaritmy z oboch strán nerovnosti zahodíme. Čo nám vo výsledku ostáva? Jednoduchá nerovnosť. Nie je ťažké to vyriešiť. X musí byť väčšie ako -0,5. Teraz skombinujeme dve získané hodnoty do systému. teda Toto bude rozsah prijateľných hodnôt pre uvažovanú logaritmickú nerovnosť. Prečo vôbec potrebujeme ODZ? Toto je príležitosť vyradiť nesprávne a nemožné odpovede. Ak odpoveď nie je v rozmedzí prijateľných hodnôt, potom odpoveď jednoducho nedáva zmysel. Toto stojí za to pamätať na dlhú dobu, pretože v jednotnej štátnej skúške je často potrebné hľadať ODZ, a to nielen logaritmických nerovností. Riešenie pozostáva z niekoľkých etáp. Najprv musíte nájsť rozsah prijateľných hodnôt. V ODZ budú dve hodnoty, o tom sme hovorili vyššie. Ďalej musíme vyriešiť samotnú nerovnosť. Metódy riešenia sú nasledovné: V závislosti od situácie sa oplatí použiť jednu z vyššie uvedených metód. Prejdime priamo k riešeniu. Prezradíme najobľúbenejšiu metódu, ktorá je vhodná na riešenie úloh Jednotnej štátnej skúšky takmer vo všetkých prípadoch. Ďalej sa pozrieme na metódu rozkladu. Môže vám pomôcť, ak narazíte na obzvlášť zákernú nerovnosť. Takže algoritmus na riešenie logaritmickej nerovnosti. Príklady riešení : Nie nadarmo sme zobrali presne túto nerovnosť! Venujte pozornosť základni. Pamätajte: ak je väčšie ako jedna, znamienko zostáva rovnaké pri hľadaní rozsahu prijateľných hodnôt; v opačnom prípade musíte zmeniť znamienko nerovnosti. V dôsledku toho dostaneme nerovnosť: Teraz zredukujeme ľavú stranu do tvaru rovnice rovnej nule. Namiesto znamienka „menej ako“ dáme „rovná sa“ a rovnicu vyriešime. Nájdeme teda ODZ. Dúfame, že s riešením takejto jednoduchej rovnice nebudete mať problémy. Odpovede sú -4 a -2. To nie je všetko. Tieto body musíte zobraziť na grafe umiestnením „+“ a „-“. Čo je pre to potrebné urobiť? Do výrazu dosaďte čísla z intervalov. Ak sú hodnoty kladné, dáme tam „+“. Odpoveď: x nemôže byť väčšie ako -4 a menšie ako -2. Našli sme rozsah prijateľných hodnôt iba pre ľavú stranu, teraz musíme nájsť rozsah prijateľných hodnôt pre pravú stranu. Toto je oveľa jednoduchšie. odpoveď: -2. Pretíname obe výsledné oblasti. A až teraz sa začíname zaoberať samotnou nerovnosťou. Zjednodušme si to čo najviac, aby sa to ľahšie riešilo. Pri riešení opäť používame intervalovú metódu. Preskočme výpočty; všetko je jasné z predchádzajúceho príkladu. Odpoveď. Táto metóda je však vhodná, ak má logaritmická nerovnosť rovnaké základy. Riešenie logaritmických rovníc a nerovníc s rôznymi základňami vyžaduje počiatočnú redukciu na rovnakú základňu. Ďalej použite metódu opísanú vyššie. Existuje však komplikovanejší prípad. Zoberme si jeden z najkomplexnejších typov logaritmických nerovností. Ako vyriešiť nerovnosti s takýmito charakteristikami? Áno, a takýchto ľudí možno nájsť v Jednotnej štátnej skúške. Riešenie nerovností nasledujúcim spôsobom priaznivo ovplyvní aj váš vzdelávací proces. Pozrime sa na problematiku podrobne. Zahoďme teóriu a prejdime rovno k praxi. Na vyriešenie logaritmických nerovností sa stačí zoznámiť s príkladom raz. Na vyriešenie logaritmickej nerovnosti prezentovaného tvaru je potrebné zredukovať pravú stranu na logaritmus s rovnakým základom. Princíp pripomína ekvivalentné prechody. V dôsledku toho bude nerovnosť vyzerať takto. V skutočnosti zostáva len vytvoriť systém nerovností bez logaritmov. Pomocou racionalizačnej metódy sa dostávame k ekvivalentnému systému nerovností. Samotnému pravidlu porozumiete, keď nahradíte príslušné hodnoty a budete sledovať ich zmeny. Systém bude mať nasledujúce nerovnosti. Pri používaní racionalizačnej metódy pri riešení nerovností si musíte zapamätať nasledovné: jeden musí byť odčítaný od základne, x sa podľa definície logaritmu odčíta od oboch strán nerovnosti (sprava zľava), dva výrazy sa násobia a nastavte pod pôvodným znamienkom vo vzťahu k nule. Ďalšie riešenie sa vykonáva pomocou intervalovej metódy, tu je všetko jednoduché. Je dôležité, aby ste pochopili rozdiely v metódach riešenia, potom všetko začne ľahko fungovať. V logaritmických nerovnostiach je veľa nuancií. Najjednoduchšie z nich sa dajú celkom ľahko vyriešiť. Ako môžete vyriešiť každý z nich bez problémov? Všetky odpovede ste už dostali v tomto článku. Teraz máte pred sebou dlhú prax. Neustále trénujte riešenie rôznych problémov na skúške a budete môcť získať najvyššie skóre. Veľa šťastia vo vašej náročnej úlohe! Definícia logaritmu Najjednoduchší spôsob, ako to napísať matematicky, je: Definícia logaritmu môže byť napísaná iným spôsobom: Venujte pozornosť obmedzeniam, ktoré sú uložené na základe logaritmu ( a) a na sublogaritmický výraz ( X). V budúcnosti sa tieto podmienky zmenia na dôležité obmedzenia pre OD, ktoré bude potrebné vziať do úvahy pri riešení akejkoľvek rovnice s logaritmami. Takže teraz treba okrem štandardných podmienok vedúcich k obmedzeniu ODZ (kladnosť výrazov pod párnymi mocninami, nerovný menovateľ k nule a pod.) zohľadniť aj tieto podmienky: Všimnite si, že ani základ logaritmu ani sublogaritmický výraz sa nemôže rovnať nule. Upozorňujeme tiež, že samotná hodnota logaritmu môže nadobúdať všetky možné hodnoty, t.j. Logaritmus môže byť kladný, záporný alebo nulový. Logaritmy majú mnoho rôznych vlastností, ktoré vyplývajú z vlastností mocničiek a definície logaritmu. Poďme si ich vymenovať. Takže vlastnosti logaritmov: Logaritmus produktu: Logaritmus zlomku: Vyberanie stupňa zo znamienka logaritmu: Venujte zvláštnu pozornosť tým z posledných uvedených vlastností, v ktorých sa po získaní stupňa objaví znamienko modulu. Nezabudnite, že pri umiestnení párneho mocniny mimo znamienka logaritmu, pod logaritmus alebo na základňu, musíte opustiť znamienko modulu. Ďalšie užitočné vlastnosti logaritmov: Posledná vlastnosť sa veľmi často používa v zložitých logaritmických rovniciach a nerovniciach. Treba si ho pripomínať rovnako ako všetkých ostatných, hoci sa naňho často zabúda. Najjednoduchšie logaritmické rovnice sú: A ich riešenie je dané vzorcom, ktorý priamo vyplýva z definície logaritmu: Ďalšie jednoduché logaritmické rovnice sú tie, ktoré možno pomocou algebraických transformácií a vyššie uvedených vzorcov a vlastností logaritmov zredukovať do tvaru: Riešenie takýchto rovníc s prihliadnutím na ODZ je nasledovné: Niektorí iní logaritmické rovnice s premennou na báze možno zredukovať na tvar: V takýchto logaritmických rovniciach všeobecný tvar riešenia tiež vyplýva priamo z definície logaritmu. Iba v tomto prípade existujú ďalšie obmedzenia pre DZ, ktoré je potrebné vziať do úvahy. Výsledkom je, že na vyriešenie logaritmickej rovnice s premennou v základe musíte vyriešiť nasledujúci systém: Pri riešení zložitejších logaritmických rovníc, ktoré nemožno redukovať na jednu z vyššie uvedených rovníc, sa tiež aktívne používa variabilná náhradná metóda. Ako obvykle, pri použití tejto metódy treba pamätať na to, že po zavedení náhrady by sa rovnica mala zjednodušiť a už neobsahovať starú neznámu. Musíte tiež pamätať na vykonanie spätnej substitúcie premenných. Niekedy pri riešení logaritmických rovníc musíte tiež použiť grafická metóda. Táto metóda spočíva v čo najpresnejšom zostrojení grafov funkcií, ktoré sú na ľavej a pravej strane rovnice na jednej súradnicovej rovine a následnom nájdení súradníc ich priesečníkov z výkresu. Takto získané korene je potrebné skontrolovať substitúciou do pôvodnej rovnice. Často je tiež užitočný pri riešení logaritmických rovníc. metóda zoskupovania. Pri použití tejto metódy je dôležité pamätať na to, že: aby sa súčin viacerých faktorov rovnal nule, je potrebné, aby sa aspoň jeden z nich rovnal nule, a zvyšok existoval. Keď sú faktory logaritmy alebo zátvorky s logaritmami, a nielen zátvorky s premennými ako v racionálnych rovniciach, môže dôjsť k mnohým chybám. Pretože logaritmy majú veľa obmedzení v oblasti, kde existujú. Pri rozhodovaní sústavy logaritmických rovníc najčastejšie musíte použiť buď substitučnú metódu alebo metódu nahradenia premenných. Ak takáto možnosť existuje, potom sa pri riešení systémov logaritmických rovníc treba snažiť zabezpečiť, aby každá z rovníc systému bola individuálne privedená do tvaru, v ktorom bude možné vykonať prechod z logaritmickej rovnice na racionálny. Najjednoduchšie logaritmické nerovnosti sa riešia približne rovnakým spôsobom ako podobné rovnice. Po prvé, pomocou algebraických transformácií a vlastností logaritmov sa ich musíme pokúsiť dostať do tvaru, kde logaritmy na ľavej a pravej strane nerovnosti budú mať rovnaké základy, t.j. získajte nerovnosť tvaru: Potom musíte prejsť na racionálnu nerovnosť, berúc do úvahy, že tento prechod by sa mal vykonať nasledovne: ak je základ logaritmu väčší ako jedna, potom sa znamienko nerovnosti nemusí meniť a ak základ logaritmu je menší ako jedna, potom musíte zmeniť znamienko nerovnosti na opačné (to znamená zmeniť "menej" na "viac" alebo naopak). V tomto prípade nie je potrebné meniť znamienka mínus na plus, obísť predtým naučené pravidlá. Zapíšme si matematicky, čo dostaneme ako výsledok vykonania takéhoto prechodu. Ak je základ väčší ako jedna, dostaneme: Ak je základ logaritmu menší ako jedna, zmeníme znamienko nerovnosti a dostaneme nasledujúci systém: Ako vidíme, pri riešení logaritmických nerovností sa ako obvykle berie do úvahy aj ODZ (toto je tretia podmienka vo vyššie uvedených systémoch). Navyše v tomto prípade nie je možné vyžadovať kladnosť oboch sublogaritmických výrazov, ale skôr iba kladnosť menšieho z nich. Pri rozhodovaní logaritmické nerovnosti s premennou v základni logaritmus, je potrebné nezávisle zvážiť obe možnosti (keď je základ menší ako jedna a väčší ako jedna) a spojiť riešenia týchto prípadov do súboru. Zároveň nesmieme zabudnúť na DL, t.j. o tom, že základ aj všetky sublogaritmické výrazy musia byť kladné. Takže pri riešení nerovnice tvaru: Získame nasledujúcu sadu systémov: Zložitejšie logaritmické nerovnosti je možné riešiť aj pomocou zmien premenných. Niektoré ďalšie logaritmické nerovnosti (ako napríklad logaritmické rovnice) vyžadujú na vyriešenie postup, pri ktorom sa logaritmus oboch strán nerovnosti alebo rovnice prenesie do rovnakého základu. Takže pri vykonávaní takéhoto postupu s logaritmickými nerovnosťami existuje jemnosť. Upozorňujeme, že pri logaritmoch so základom väčším ako jedna sa znamienko nerovnosti nemení, ale ak je základ menší ako jedna, znamienko nerovnosti sa obráti. Ak logaritmickú nerovnosť nemožno redukovať na racionálnu alebo vyriešiť pomocou substitúcie, potom v tomto prípade treba použiť zovšeobecnená intervalová metóda, ktorá je nasledovná: Pre úspešnú prípravu na CT z fyziky a matematiky je okrem iného potrebné splniť tri najdôležitejšie podmienky: Úspešná, usilovná a zodpovedná implementácia týchto troch bodov vám umožní ukázať sa na CT výborný výsledok, maximum toho, čoho ste schopní. Ak si myslíte, že ste našli chybu v vzdelávacie materiály, potom o tom prosím napíšte e-mailom. Môžete tiež nahlásiť chybu na sociálna sieť(). V liste uveďte predmet (fyziku alebo matematiku), názov alebo číslo témy alebo testu, číslo úlohy, prípadne miesto v texte (strane), kde je podľa vás chyba. Popíšte tiež, o akú chybu ide. Váš list nezostane nepovšimnutý, chyba bude buď opravená, alebo vám bude vysvetlené, prečo nejde o chybu.

Príklady riešenia
![]()



3x > 24;
x > 8. ![]()
Čo je potrebné na riešenie logaritmických nerovností?
Domáca úloha

B) Predstavte (ak je to možné) ľavú a pravú stranu nerovnosti ako logaritmy na rovnakú základňu.
C) Určte, či je logaritmická funkcia rastúca alebo klesajúca: ak t>1, potom rastúca; ak 0
D) Prejdite na jednoduchšiu nerovnosť (sublogaritmické výrazy), pričom vezmite do úvahy, že znamienko nerovnosti zostane rovnaké, ak sa funkcia zvýši, a zmení sa, ak sa zníži.
KĽÚČ: 13321, maximálny počet bodov – 6 bodov.





Teraz, keď sme sa zoznámili s pojmami jednotlivo, prejdime k ich všeobecnému zváženiu.

čo je ODZ? ODZ pre logaritmické nerovnosti

Teraz prejdime k riešeniu najjednoduchšej logaritmickej nerovnosti.


Algoritmus na riešenie logaritmickej nerovnosti





Logaritmické nerovnosti s premenlivou základňou






![]()
![]()

![]()

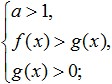


Ako sa úspešne pripraviť na CT z fyziky a matematiky?
Našli ste chybu?




