Biz matematikani tanlamaymiz uning kasbi va u bizni tanlaydi.
Rus matematigi Yu.I. Manin
Modulli tenglamalar
Maktab matematikasida yechishning eng qiyin masalalari modul belgisi ostida o'zgaruvchilarni o'z ichiga olgan tenglamalardir. Bunday tenglamalarni muvaffaqiyatli yechish uchun siz modulning ta'rifi va asosiy xususiyatlarini bilishingiz kerak. Tabiiyki, talabalar bu turdagi tenglamalarni yechish ko'nikmalariga ega bo'lishlari kerak.
Asosiy tushunchalar va xususiyatlar
Haqiqiy sonning moduli (mutlaq qiymati). bilan belgilanadi va quyidagicha aniqlanadi:
TO oddiy xususiyatlar modul quyidagi munosabatlarni o'z ichiga oladi:
Eslatma, oxirgi ikki xususiyat har qanday juft daraja uchun amal qiladi.
Bundan tashqari, agar, qaerda, keyin va
Ko'proq murakkab xususiyatlar modul, modulli tenglamalarni yechishda unumli foydalanish mumkin, quyidagi teoremalar orqali ifodalanadi:
Teorema 1.Har qanday analitik funktsiyalar uchun Va tengsizlik haqiqatdir
Teorema 2. Tenglik tengsizlikka tengdir.
Teorema 3. Tenglik tengsizlikka teng.
Keling, “Tenglamalar, modul belgisi ostida o'zgaruvchilarni o'z ichiga olgan."
Modulli tenglamalarni yechish
Maktab matematikasida modulli tenglamalarni yechishning eng keng tarqalgan usuli bu usuldir, modulni kengaytirishga asoslangan. Ushbu usul universaldir, ammo, umumiy holatda, uni ishlatish juda og'ir hisob-kitoblarga olib kelishi mumkin. Shu munosabat bilan talabalar boshqalarni bilishlari kerak, Ko'proq samarali usullar va bunday tenglamalarni yechish texnikasi. Ayniqsa, teoremalarni qo'llash ko'nikmalariga ega bo'lish kerak, ushbu maqolada berilgan.
1-misol. Tenglamani yeching. (1)
Yechim. Biz (1) tenglamani "klassik" usul - modullarni ochish usuli yordamida hal qilamiz. Buning uchun sonlar o'qini ajratamiz nuqta va intervallarga ajrating va uchta holatni ko'rib chiqing.
1. Agar , , , va tenglama (1) shaklni oladi. Bundan kelib chiqadi. Biroq, bu erda , shuning uchun topilgan qiymat (1) tenglamaning ildizi emas.
2. Agar, keyin (1) tenglamadan olamiz yoki .
O'shandan beri (1) tenglamaning ildizi.
3. Agar, u holda (1) tenglama shaklni oladi yoki . Shuni ta'kidlab o'tamiz.
Javob: , .
Keyingi tenglamalarni modul yordamida yechishda biz bunday tenglamalarni yechish samaradorligini oshirish uchun modullarning xossalaridan faol foydalanamiz.
2-misol. Tenglamani yeching.
Yechim. O'shandan beri va keyin tenglamadan kelib chiqadi. Ushbu munosabatda, , , va tenglama shaklni oladi. Bu erdan olamiz. Biroq, shuning uchun asl tenglamaning ildizlari yo'q.
Javob: ildiz yo'q.
3-misol. Tenglamani yeching.
Yechim. O'shandan beri. Agar , keyin va tenglama shaklni oladi.
Bu erdan olamiz.
4-misol. Tenglamani yeching.
Yechim.Keling, tenglamani ekvivalent shaklda qayta yozamiz. (2)
Olingan tenglama turdagi tenglamalarga tegishli.
2-teoremani hisobga olgan holda, (2) tenglama tengsizlikka ekvivalent ekanligini ta'kidlash mumkin. Bu erdan olamiz.
Javob: .
5-misol. Tenglamani yeching.
Yechim. Bu tenglama shaklga ega. Shunung uchun , 3-teoremaga muvofiq, bu erda biz tengsizlikka egamiz yoki .
6-misol. Tenglamani yeching.
Yechim. Buni taxmin qilaylik. Chunki, u holda berilgan tenglama kvadrat tenglama shaklini oladi, (3)
Qayerda . Chunki (3) tenglama bitta musbat ildizga ega undan keyin . Bu yerdan biz asl tenglamaning ikkita ildizini olamiz: Va .
7-misol. Tenglamani yeching. (4)
Yechim. Tenglamadan beriikki tenglamaning birikmasiga teng: Va , u holda (4) tenglamani yechishda ikkita holatni ko'rib chiqish kerak.
1. Agar , keyin yoki .
Bu yerdan biz , va .
2. Agar , keyin yoki .
O'shandan beri.
Javob: , , , .
8-misol.Tenglamani yeching . (5)
Yechim. O'shandan beri va, keyin. Bu yerdan va (5) tenglamadan shunday va , ya'ni. bu yerda tenglamalar tizimi mavjud
Biroq bu tizim tenglamalar mos kelmaydi.
Javob: ildiz yo'q.
9-misol. Tenglamani yeching. (6)
Yechim. Agar ni belgilasak, u holda va (6) tenglamadan olamiz
Yoki . (7)
(7) tenglama ko'rinishga ega bo'lgani uchun bu tenglama tengsizlikka ekvivalentdir. Bu erdan olamiz. O'shandan beri, keyin yoki.
Javob: .
10-misol.Tenglamani yeching. (8)
Yechim.1-teoremaga binoan biz yozishimiz mumkin
(9)
(8) tenglikni hisobga olib, biz ikkala tengsizlik (9) tenglikka aylanadi degan xulosaga kelamiz, ya'ni. tenglamalar tizimi mavjud
Biroq, 3-teoremaga ko'ra, yuqoridagi tenglamalar tizimi tengsizliklar tizimiga ekvivalentdir.
(10)
Tengsizliklar tizimini yechish (10) ga erishamiz. (10) tengsizliklar sistemasi (8) tenglamaga ekvivalent bo'lganligi sababli, dastlabki tenglama bitta ildizga ega.
Javob: .
11-misol. Tenglamani yeching. (11)
Yechim. va bo'lsin, u holda (11) tenglamadan tenglik kelib chiqadi.
Bundan kelib chiqadi va . Shunday qilib, bu erda biz tengsizliklar tizimiga egamiz
Bu tengsizliklar tizimining yechimi Va .
Javob: , .
12-misol.Tenglamani yeching. (12)
Yechim. (12) tenglama modullarni ketma-ket kengaytirish usuli bilan yechiladi. Buning uchun bir nechta holatlarni ko'rib chiqamiz.
1. Agar , keyin .
1.1. Agar , keyin va ,.
1.2. Agar, keyin. Biroq, shuning uchun ichida Ushbu holatda(12) tenglamaning ildizlari yo'q.
2. Agar , keyin .
2.1. Agar , keyin va ,.
2.2. Agar , keyin va.
Javob: , , , , .
13-misol.Tenglamani yeching. (13)
Yechim.(13) tenglamaning chap tomoni manfiy bo'lmagani uchun . Shu munosabat bilan va tenglama (13)
yoki shaklini oladi.
Ma'lumki, tenglama ikki tenglamaning birikmasiga teng Va , biz erishgan narsani hal qilish, . Chunki, u holda (13) tenglama bitta ildizga ega.
Javob: .
14-misol. Tenglamalar tizimini yechish (14)
Yechim. Buyon va , keyin va . Shunday qilib, (14) tenglamalar tizimidan biz to'rtta tenglamalar tizimini olamiz:
Yuqoridagi tenglamalar sistemalarining ildizlari tenglamalar sistemasining ildizlari (14).
Javob: ,, , , , , , .
15-misol. Tenglamalar tizimini yechish (15)
Yechim. O'shandan beri. Shu munosabat bilan (15) tenglamalar tizimidan ikkita tenglamalar tizimini olamiz
Birinchi tenglamalar sistemasining ildizlari va , ikkinchi tenglamalar tizimidan esa va ni olamiz.
Javob: , , , .
16-misol. Tenglamalar tizimini yechish (16)
Yechim.(16) sistemaning birinchi tenglamasidan kelib chiqadiki.
O'shandan beri . Tizimning ikkinchi tenglamasini ko'rib chiqamiz. Chunki, Bu, va tenglama shaklni oladi, , yoki .
Agar siz qiymatni almashtirsangizsistemaning birinchi tenglamasiga (16), keyin yoki .
Javob: , .
Muammoni hal qilish usullarini chuqurroq o'rganish uchun, tenglamalarni yechish bilan bog’liq, modul belgisi ostida o'zgaruvchilarni o'z ichiga olgan, Tavsiya etilgan adabiyotlar ro'yxatidan o'quv qo'llanmalarini tavsiya qilishingiz mumkin.
1. Kollejlarga abituriyentlar uchun matematikadan masalalar to'plami / Ed. M.I. Skanavi. - M.: Tinchlik va ta'lim, 2013. – 608 b.
2. Suprun V.P. O'rta maktab o'quvchilari uchun matematika: murakkablikdagi vazifalar. – M.: "Librocom" CD / URSS, 2017. – 200 b.
3. Suprun V.P. O'rta maktab o'quvchilari uchun matematika: muammolarni hal qilishning nostandart usullari. – M.: "Librocom" CD / URSS, 2017. – 296 b.
Hali ham savollaringiz bormi?
Repetitordan yordam olish uchun ro'yxatdan o'ting.
veb-sayt, materialni to'liq yoki qisman nusxalashda manbaga havola talab qilinadi.
Eng biri qiyin mavzular talabalar uchun modul belgisi ostida o'zgaruvchini o'z ichiga olgan tenglamalarni yechishdir. Avval bilib olaylik, bu nima bilan bog'liq? Nega, masalan, ko'pchilik bolalar kvadrat tenglamalarni yong'oq kabi buzadilar, lekin modul kabi murakkab tushunchadan yiroqda juda ko'p muammolarga duch kelishadi?
Menimcha, bu qiyinchiliklarning barchasi modulli tenglamalarni echish uchun aniq tuzilgan qoidalarning yo'qligi bilan bog'liq. Shunday qilib, qaror qabul qilish kvadrat tenglama, talaba birinchi navbatda diskriminant formulasini, keyin esa kvadrat tenglamaning ildizlari uchun formulalarni qo'llash kerakligini aniq biladi. Agar tenglamada modul topilsa nima qilish kerak? Biz aniq tasvirlashga harakat qilamiz zarur reja Tenglama modul belgisi ostida noma'lum bo'lsa, harakatlar. Har bir holat uchun bir nechta misollar keltiramiz.
Lekin birinchi navbatda, eslaylik modul ta'rifi. Shunday qilib, raqamni modul qiling a bu raqamning o'zi if deb ataladi a salbiy bo'lmagan va -a, agar raqam a noldan kam. Siz buni shunday yozishingiz mumkin:
|a| = a, agar a ≥ 0 va |a| = -a agar a< 0
Modulning geometrik ma'nosi haqida gapirganda, har bir haqiqiy raqam ma'lum bir nuqtaga to'g'ri kelishini yodda tutish kerak. raqam o'qi- unga 
muvofiqlashtirish. Demak, sonning moduli yoki mutlaq qiymati bu nuqtadan raqamli o‘qning boshigacha bo‘lgan masofadir. Masofa har doim ijobiy raqam sifatida belgilanadi. Shunday qilib, har qanday manfiy sonning moduli musbat sondir. Aytgancha, bu bosqichda ham ko'plab talabalar chalkashishni boshlaydilar. Modul har qanday raqamni o'z ichiga olishi mumkin, ammo moduldan foydalanish natijasi har doim ijobiy raqam bo'ladi.
Endi to'g'ridan-to'g'ri tenglamalarni echishga o'tamiz.
1. |x| ko'rinishdagi tenglamani ko'rib chiqing = c, bu erda c - haqiqiy son. Ushbu tenglamani modul ta'rifi yordamida echish mumkin.
Biz barcha haqiqiy sonlarni uch guruhga ajratamiz: noldan katta bo'lganlar, noldan kichiklari va uchinchi guruh 0 raqami. Yechimni diagramma shaklida yozamiz:
(±c, agar c > 0 bo'lsa
Agar |x| = c, keyin x = (0, agar c = 0 bo'lsa
(bilan bo'lsa, ildiz yo'q< 0
1) |x| = 5, chunki 5 > 0, keyin x = ±5;
2) |x| = -5, chunki -5< 0, то уравнение не имеет корней;
3) |x| = 0, keyin x = 0.
2. |f(x)| ko'rinishdagi tenglama = b, bu erda b > 0. Bu tenglamani yechish uchun moduldan qutulish kerak. Biz buni shunday qilamiz: f(x) = b yoki f(x) = -b. Endi siz hosil bo'lgan tenglamalarning har birini alohida echishingiz kerak. Agar dastlabki tenglamada b< 0, решений не будет.
1) |x + 2| = 4, chunki 4 > 0, keyin
x + 2 = 4 yoki x + 2 = -4
2) |x 2 – 5| = 11, chunki 11 > 0, keyin
x 2 – 5 = 11 yoki x 2 – 5 = -11
x 2 = 16 x 2 = -6
x = ± 4 ildiz yo'q
3) |x 2 – 5x| = -8, chunki -8< 0, то уравнение не имеет корней.
3. |f(x)| ko'rinishdagi tenglama = g(x). Modulning ma'nosiga ko'ra, bunday tenglama, agar uning o'ng tomoni noldan katta yoki teng bo'lsa, echimlarga ega bo'ladi, ya'ni. g(x) ≥ 0. U holda bizda:
f(x) = g(x) yoki f(x) = -g(x).
1) |2x – 1| = 5x – 10. Agar 5x – 10 ≥ 0 boʻlsa, bu tenglamaning ildizlari boʻladi. Bunday tenglamalarni yechish shu yerda boshlanadi.
1. O.D.Z. 5x – 10 ≥ 0
2. Yechim:
2x – 1 = 5x – 10 yoki 2x – 1 = -(5x – 10)
3. Biz O.D.Z ni birlashtiramiz. va yechim, biz olamiz:
Ildiz x = 11/7 O.D.Z.ga mos kelmaydi, u 2 dan kichik, lekin x = 3 bu shartni qanoatlantiradi.
Javob: x = 3
2) |x – 1| = 1 – x 2.
1. O.D.Z. 1 – x 2 ≥ 0. Bu tengsizlikni interval usuli yordamida yechamiz:
(1 – x)(1 + x) ≥ 0
2. Yechim:
x – 1 = 1 – x 2 yoki x – 1 = -(1 – x 2)
x 2 + x – 2 = 0 x 2 – x = 0
x = -2 yoki x = 1 x = 0 yoki x = 1
3. Biz eritma va O.D.Z.ni birlashtiramiz:
Faqat x = 1 va x = 0 ildizlari mos keladi.
Javob: x = 0, x = 1.
4. |f(x)| ko'rinishdagi tenglama = |g(x)|. Bunday tenglama quyidagi f(x) = g(x) yoki f(x) = -g(x) ikkita tenglamaga ekvivalentdir.
1) |x 2 – 5x + 7| = |2x – 5|. Bu tenglama quyidagi ikkitaga teng:
x 2 – 5x + 7 = 2x – 5 yoki x 2 – 5x +7 = -2x + 5
x 2 – 7x + 12 = 0 x 2 – 3x + 2 = 0
x = 3 yoki x = 4 x = 2 yoki x = 1
Javob: x = 1, x = 2, x = 3, x = 4.
5. O'zgartirish usuli bilan yechilgan tenglamalar (o'zgaruvchilarni almashtirish). Ushbu yechim usuli eng oson tushuntirilgan aniq misol. Shunday qilib, modulli kvadrat tenglama berilsin:
x 2 – 6|x| + 5 = 0. Modul xossasi bo'yicha x 2 = |x| 2, shuning uchun tenglamani quyidagicha qayta yozish mumkin:
|x| 2 – 6|x| + 5 = 0. |x| ni almashtiramiz = t ≥ 0, u holda biz quyidagilarga ega bo'lamiz:
t 2 – 6t + 5 = 0. Bu tenglamani yechib, t = 1 yoki t = 5 ekanligini topamiz. O‘zgartirishga qaytaylik:
|x| = 1 yoki |x| = 5
x = ±1 x = ±5
Javob: x = -5, x = -1, x = 1, x = 5.
Keling, yana bir misolni ko'rib chiqaylik:
x 2 + |x| – 2 = 0. Modul xossasi bo'yicha x 2 = |x| 2, shuning uchun
|x| 2 + |x| – 2 = 0. |x| ni almashtiramiz = t ≥ 0, keyin:
t 2 + t – 2 = 0. Bu tenglamani yechib, t = -2 yoki t = 1 ni olamiz. O‘zgartirishga qaytaylik:
|x| = -2 yoki |x| = 1
X = ± 1 ildiz yo'q
Javob: x = -1, x = 1.
6. Yana bir turdagi tenglamalar “murakkab” modulli tenglamalardir. Bunday tenglamalarga "modul ichidagi modullar" bo'lgan tenglamalar kiradi. Ushbu turdagi tenglamalarni modul xossalari yordamida yechish mumkin.
1) |3 – |x|| = 4. Biz ikkinchi turdagi tenglamalardagi kabi harakat qilamiz. Chunki 4 > 0, keyin ikkita tenglamani olamiz:
3 – |x| = 4 yoki 3 – |x| = -4.
Endi har bir tenglamada x modulini ifodalaymiz, keyin |x| = -1 yoki |x| = 7.
Olingan tenglamalarning har birini yechamiz. Birinchi tenglamada ildiz yo'q, chunki -1< 0, а во втором x = ±7.
Javob x = -7, x = 7.
2) |3 + |x + 1|| = 5. Bu tenglamani xuddi shunday yechamiz:
3 + |x + 1| = 5 yoki 3 + |x + 1| = -5
|x + 1| = 2 |x + 1| = -8
x + 1 = 2 yoki x + 1 = -2. Ildizlari yo'q.
Javob: x = -3, x = 1.
Modulli tenglamalarni yechishning universal usuli ham mavjud. Bu intervalli usul. Ammo keyinroq ko'rib chiqamiz.
blog.site, materialni to'liq yoki qisman nusxalashda asl manbaga havola talab qilinadi.
MBOU 17-sonli o'rta maktab, Ivanovo
« Modulli tenglamalar"
Uslubiy ishlanma
Kompilyatsiya qilingan
matematika o'qituvchisi
Lebedeva N.V.20010
Tushuntirish eslatmasi
1-bob. Kirish
Bo'lim 2. Asosiy xususiyatlar 3-bo'lim. Sonning moduli tushunchasining geometrik talqini 4-bo'lim. y = |x| funksiya grafigi 5-bo'lim. Konventsiyalar2-bob. Modulli tenglamalarni yechish
1-bo'lim. |F(x)| ko'rinishdagi tenglamalar = m (eng oddiy) 2-bo'lim. F(|x|) = m ko'rinishdagi tenglamalar 3-bo'lim. |F(x)| ko'rinishdagi tenglamalar = G(x) 4-bo'lim. |F(x)| ko'rinishdagi tenglamalar = ± F(x) (eng chiroyli) 5-bo'lim. |F(x)| ko'rinishdagi tenglamalar = |G(x)| 6-bo'lim. Nostandart tenglamalarni yechishga misollar 7-bo'lim. |F(x)| ko'rinishdagi tenglamalar + |G(x)| = 0 8-bo'lim. |a 1 x ± b 1 | ko'rinishdagi tenglamalar ± |a 2 x ± b 2 | ± …|a n x ± da n | = m 9-bo'lim. Bir nechta modullarni o'z ichiga olgan tenglamalar3-bob. Modulli har xil tenglamalarni yechishga misollar.
1-qism. Trigonometrik tenglamalar 2-qism. Eksponensial tenglamalar 3-bo'lim. Logarifmik tenglamalar 4-bo'lim. Irratsional tenglamalar 5-bo'lim. Murakkab vazifalar Mashqlar uchun javoblar Adabiyotlar ro'yxatiTushuntirish eslatmasi.
Haqiqiy sonning mutlaq qiymati (modul) tushunchasi uning muhim belgilaridan biridir. Bu tushuncha fizika, matematika va texnika fanlarining turli bo'limlarida keng tarqalgan. In matematika kurslarini o'qitish amaliyotida o'rta maktab Rossiya Federatsiyasi Mudofaa vazirligining Dasturiga muvofiq, "raqamning mutlaq qiymati" tushunchasi qayta-qayta uchraydi: 6-sinfda modulning ta'rifi va uning geometrik ma'nosi kiritiladi; 8-sinfda mutlaq xato tushunchasi shakllantiriladi, modulli eng oddiy tenglama va tengsizliklar yechimi ko‘rib chiqiladi, arifmetikaning xossalari o‘rganiladi. kvadrat ildiz; 11-sinfda tushuncha “Ildiz n- daraja." O'qitish tajribasi shuni ko'rsatadiki, talabalar ko'pincha ushbu materialni bilishni talab qiladigan vazifalarni hal qilishda qiyinchiliklarga duch kelishadi va ko'pincha ularni bajarishni boshlamasdan ularni o'tkazib yuborishadi. 9 va 11-sinf kurslari uchun imtihon topshiriqlari matnlarida ham shu kabi topshiriqlar mavjud. Bundan tashqari, universitetlarning maktab bitiruvchilariga qo'yadigan talablari farqlanadi, ya'ni ko'proq yuqori daraja maktab o'quv dasturi talablariga nisbatan. Zamonaviy jamiyatda hayot uchun ma'lum aqliy qobiliyatlarda namoyon bo'ladigan matematik fikrlash uslubini shakllantirish juda muhimdir. Modullar bilan masalalarni yechish jarayonida umumlashtirish va spetsifikatsiya qilish, tahlil qilish, tasniflash va tizimlashtirish, analogiya kabi usullardan foydalana bilish talab etiladi. Bunday vazifalarni hal qilish asosiy bo'limlar bo'yicha bilimlaringizni sinab ko'rish imkonini beradi maktab kursi, Daraja mantiqiy fikrlash, dastlabki tadqiqot qobiliyatlari. bu ish bo'limlardan biriga - modulni o'z ichiga olgan tenglamalarni echishga bag'ishlangan. U uchta bobdan iborat. Birinchi bobda asosiy tushunchalar va eng muhim nazariy fikrlar keltirilgan. Ikkinchi bobda modulni o'z ichiga olgan to'qqizta asosiy tenglama turi taklif etiladi, ularni yechish usullari muhokama qilinadi va turli darajadagi murakkablik misollari ko'rib chiqiladi. Uchinchi bobda murakkabroq va nostandart tenglamalar (trigonometrik, eksponensial, logarifmik va irratsional) keltirilgan. Har bir tenglama turi uchun mashqlar mavjud mustaqil qaror(javoblar va ko'rsatmalar ilova qilinadi). Bu ishning asosiy maqsadi o‘qituvchilarga darsga tayyorgarlik ko‘rishda va fakultiv kurslarni tashkil etishda uslubiy yordam ko‘rsatishdan iborat. Material sifatida ham foydalanish mumkin o'quv yordami o'rta maktab o'quvchilari uchun. Ishda taklif etilgan vazifalar qiziqarli va har doim ham oson emas, bu o'quvchilarning ta'lim motivatsiyasini yanada ongli qilish, ularning qobiliyatlarini sinab ko'rish va maktab bitiruvchilarini oliy o'quv yurtlariga kirishga tayyorlash darajasini oshirish imkonini beradi. Taklif etilayotgan mashqlarning tabaqalashtirilgan tanlovi materialni o'zlashtirishning reproduktiv darajasidan ijodiy darajaga o'tishni, shuningdek, nostandart muammolarni hal qilishda bilimlaringizni qanday qo'llashni o'rgatish imkoniyatini o'z ichiga oladi.1-bob. Kirish.
1-bo'lim. Mutlaq qiymatni aniqlash .
Ta'rif : Haqiqiy sonning mutlaq qiymati (modul). A manfiy bo'lmagan raqam deyiladi: A yoki -A. Belgilash: │ A │ Yozuv quyidagicha o'qiladi: "a sonining moduli" yoki "a sonining mutlaq qiymati"│ a, agar a > 0 bo'lsa
│a│ = │ 0, agar a = 0 (1)
│ - va agar aMisollar: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1
- Ifoda modulini kengaytirish:
Bo'lim 2. Asosiy xususiyatlar.
Mutlaq qiymatning asosiy xossalarini ko'rib chiqamiz. №1 mulk: Qarama-qarshi raqamlar teng modullarga ega, ya'ni. │a│=│- a│ Keling, tenglik to'g'ri ekanligini ko'rsataylik. Keling, sonning ta'rifini yozamiz - A : │- a│= (2) (1) va (2) to'plamlarni solishtiramiz. Ko'rinib turibdiki, ta'riflar mutlaq qiymatlar raqamlar A Va - A mos kelish. Demak, │a│=│- a│Quyidagi xususiyatlarni ko'rib chiqayotganda, biz ularning formulasi bilan cheklanamiz, chunki ularning isboti keltirilgan №2 mulk: Cheklangan sonli haqiqiy sonlar yig‘indisining mutlaq qiymati atamalarning mutlaq qiymatlari yig‘indisidan oshmaydi: │a 1 + a 2 +…+ a n │ ≤│a 1 │+│a 2 │ + … + │a n │ №3 mulk: Ikki haqiqiy son orasidagi farqning mutlaq qiymati ularning mutlaq qiymatlari yig'indisidan oshmaydi: │a - v│ ≤│a│+│v│ №4 mulk: Haqiqiy sonlarning cheklangan soni ko'paytmasining mutlaq qiymati omillarning mutlaq qiymatlari ko'paytmasiga teng: │a·v│=│a│·│v│ №5 mulk: Haqiqiy sonlar qismining mutlaq qiymati ularning mutlaq qiymatlari qismiga teng:
3-bo'lim. Sonning moduli tushunchasining geometrik talqini.
Har bir haqiqiy sonni raqamlar chizig'idagi nuqta bilan bog'lash mumkin, bu haqiqiy sonning geometrik tasviri bo'ladi. Raqam chizig'idagi har bir nuqta uning boshlang'ich nuqtasidan masofasiga to'g'ri keladi, ya'ni. segmentning boshidan berilgan nuqtagacha bo'lgan uzunligi. Bu masofa har doim salbiy bo'lmagan qiymat sifatida qabul qilinadi. Shuning uchun tegishli segmentning uzunligi berilgan haqiqiy sonning mutlaq qiymatining geometrik talqini bo'ladi
Taqdim etilgan geometrik rasm 1-sonli mulkni aniq tasdiqlaydi, ya'ni. qarama-qarshi sonlarning modullari teng. Bu yerdan tenglikning haqiqiyligi oson tushuniladi: │x – a│= │a – x│. │x│= m tenglamaning yechimi ham aniqroq bo'ladi, bu erda m ≥ 0, ya'ni x 1,2 = ± m. Misollar: 1) │x│= 4 x 1,2 = ± 4 2) │x - 3│= 1
x 1,2 = 2; 4 4-bo'lim. y = │x│ funksiyaning grafigi
Bu funksiyaning sohasi barcha haqiqiy sonlardir.5-bo'lim. Konventsiyalar.
Kelajakda tenglamalarni echish misollarini ko'rib chiqishda quyidagilar qo'llaniladi shartli belgilar: ( - tizim belgisi [ - umumiylik belgisi Tenglamalar (tengsizliklar) tizimini yechishda tizimga kiritilgan tenglamalar (tengsizliklar) yechimlarining kesishuvi topiladi. Tenglamalar (tengsizliklar) to‘plamini yechishda tenglamalar (tengsizliklar) to‘plamiga kiritilgan yechimlar birligi topiladi.2-bob. Modulli tenglamalarni yechish.
Ushbu bobda biz bir yoki bir nechta modulli tenglamalarni echishning algebraik usullarini ko'rib chiqamiz.1-bo'lim. │F (x)│= m ko'rinishdagi tenglamalar
Bunday turdagi tenglama eng oddiy deb ataladi. Agar m ≥ 0 bo'lsa, u yechimga ega. Modulning ta'rifiga ko'ra, dastlabki tenglama ikkita tenglama to'plamiga ekvivalentdir: │ F(x)│=m
Misollar:
№1. Tenglamani yeching: │7x - 2│= 9
Javob: x 1
= - 1; X 2
= 1
4
/
7
№2
│x 2 + 3x + 1│= 1
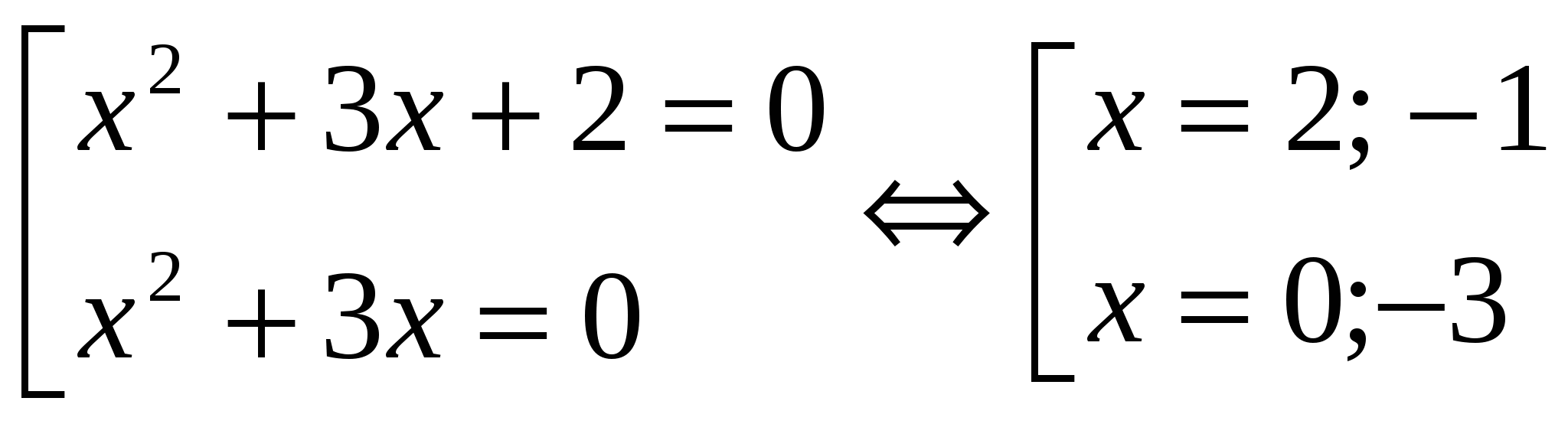x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x 2 = -3 Javob: ildizlarning yig'indisi - 2 ga teng.№3
│x 4 -5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0 x 2 = m, m ≥ 0 x = 0 ni bildiradi; ±√5 m 2 - 5m + 4 = 0 m = 1; 4 – ikkala qiymat ham m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 shartni qondiradi Javob: 7-tenglamaning ildizlari soni. Mashqlar:
№1. Tenglamani yeching va ildizlar yig‘indisini ko‘rsating: │x - 5│= 3 №2 . Tenglamani yeching va kichikroq ildizni ko'rsating: │x 2 + x│= 0 №3 . Tenglamani yeching va kattaroq ildizni ko‘rsating: │x 2 – 5x + 4│= 4 №4 .Tenglamani yeching va butun ildizni ko‘rsating: │2x 2 – 7x + 6│= 1 №5 .Tenglamani yeching va ildizlar sonini ko‘rsating: │x 4 – 13x 2 + 50│= 14
2-bo'lim. F(│x│) = m ko'rinishdagi tenglamalar
Chap tomondagi funktsiya argumenti modul belgisi ostida, o'ng tomoni esa o'zgaruvchidan mustaqil. Ushbu turdagi tenglamalarni yechishning ikkita usulini ko'rib chiqamiz. 1 usul: Mutlaq qiymat ta'rifiga ko'ra, dastlabki tenglama ikki tizimning kombinatsiyasiga tengdir. Ularning har birida submodulyar ifodaga shart qo'yiladi. F(│x│) =m
F(│x│) funksiya butun ta’rif sohasi bo‘ylab juft bo‘lgani uchun F(x) = m va F(- x) = m tenglamalarning ildizlari qarama-qarshi sonlar juftligidir. Shuning uchun tizimlardan birini hal qilish kifoya (misollarni shu tarzda ko'rib chiqishda bitta tizimning echimi beriladi). 2-usul: Yangi o'zgaruvchini kiritish usulini qo'llash. Bunda │x│= a belgisi kiritiladi, bunda a ≥ 0. Bu usul dizaynda kamroq hajmli. Misollar: №1 . Tenglamani yeching: 3x 2 – 4│x│= - 1 Yangi oʻzgaruvchining kiritilishidan foydalanamiz. │x│= a ni belgilaymiz, bu erda a ≥ 0. 3a tenglamani olamiz 2 - 4a + 1 = 0 D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 Dastlabki o'zgaruvchiga qaytish: │ x│=1 va │x│= 1/3. Har bir tenglamaning ikkita ildizi bor. Javob: x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Tenglamani yeching: 5x 2 + 3│x│- 1 = 1 / 2 │x│ + 3x 2
Populyatsiyaning birinchi sistemasi yechimini topamiz: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 E'tibor bering, x 2 ni qanoatlantirmaydi. shart x ≥ 0. Yechish ikkinchi sistema x 1 qiymatiga qarama-qarshi son bo'ladi. Javob: x 1
=
-5+√57
/
8
; X 2
=
5-√57
/
8
.№3
.
Tenglamani yeching: x 4 – │x│= 0 │x│= a ni belgilaymiz, bu yerda a ≥ 0. a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 tenglamani olamiz. a 2 = 1 Asl o'zgaruvchiga qaytish: │x│=0 va │x│= 1 x = 0; ± 1 Javob: x 1
= 0; X 2
= 1; X 3
= - 1.
Mashqlar: №6. Tenglamani yeching: 2│x│ - 4,5 = 5 – 3 / 8 │x│ №7 . Tenglamani yeching, javobingizdagi ildizlar sonini ko'rsating: 3x 2 - 7│x│ + 2 = 0 №8 . Tenglamani yeching, javobingizda butun sonlarni ko'rsating: x 4 + │x│ - 2 = 0
3-bo'lim. │F(x)│ = G(x) ko'rinishdagi tenglamalar
Bu tipdagi tenglamaning o‘ng tomoni o‘zgaruvchiga bog‘liq va shuning uchun yechimga ega bo‘ladi, agar o‘ng tomoni G(x) ≥ 0 funksiya bo‘lsagina. Asl tenglamani ikki usulda yechish mumkin. : 1 usul: Standart, uning ta'rifiga asoslangan modulni ochishga asoslangan va ikkita tizimning kombinatsiyasiga ekvivalent o'tishdan iborat. │ F(x)│ =G(X)
Bu usuldan G(x) funksiya uchun kompleks ifoda va F(x) funksiya uchun unchalik murakkab bo‘lmagan ifodada oqilona foydalanish mumkin, chunki F(x) funksiyali tengsizliklar yechiladi deb faraz qilingan. 2-usul: O'ng tomonda shart qo'yilgan ekvivalent tizimga o'tishdan iborat. │ F(x)│=
G(x)
Agar G(x) funksiyaning ifodasi F(x) funksiyasiga nisbatan murakkabroq boʻlsa, bu usuldan foydalanish qulayroqdir, chunki G(x) ≥ 0 tengsizligining yechimi Qoʻshimcha holatda qabul qilinadi bir nechta modullardan ikkinchi variantdan foydalanish tavsiya etiladi. Misollar:
№1.
Tenglamani yeching: │x + 2│= 6 -2x 
(1 yo'l) Javob: x = 1 1
/
3
№2.
│x 2 – 2x - 1│= 2·(x + 1)
(2 tomonlama) Javob: Ildizlarning hosilasi 3 ga teng.№3. Tenglamani yeching va javobingizdagi ildizlar yig‘indisini ko‘rsating:
│x - 6│= x 2 - 5x + 9
Javob: ildizlarning yig'indisi 4 ga teng.
Mashqlar: №9. │x + 4│= - 3x №10. Tenglamani yeching, javobingizdagi yechimlar sonini ko‘rsating:│x 2 + x - 1│= 2x – 1 №11 . Tenglamani yeching, javobingizda ildizlarning ko‘paytmasini ko‘rsating:│x + 3│= x 2 + x – 6
4-bo'lim. │F(x)│= F(x) va │F(x)│= - F(x) ko'rinishdagi tenglamalar
Ushbu turdagi tenglamalar ba'zan "eng chiroyli" deb ataladi. Tenglamalarning o'ng tomoni o'zgaruvchiga bog'liq bo'lganligi sababli, echimlar faqat o'ng tomoni manfiy bo'lmagan taqdirdagina mavjud bo'ladi. Shunday qilib, dastlabki tenglamalar tengsizliklarga ekvivalentdir:│F(x)│= F(x) F(x) ≥ 0 va │F(x)│= - F(x) F(x) Misollar: №1 . Tenglamani yeching, javobingizda kichikroq butun son ildizini ko'rsating: │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Javob: x = 1№2. Tenglamani yeching, javobingizdagi oraliq uzunligini ko'rsating: │x 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3; 3] Javob: oraliq uzunligi 6 ga teng.№3 . Tenglamani yeching va javobingizdagi butun yechimlar sonini ko‘rsating: │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] Javob: 4 ta butun yechim.№4 . Tenglamani yeching va javobingizdagi eng katta ildizni ko'rsating:
│4 – x -
│= 4 – x – 
x 2 – 5x + 5 = 0 D = 5 x 1,2 = 
≈ 1,4Javob: x = 3.
Mashqlar:
№12.
Tenglamani yeching, javobingizda butun ildizni ko'rsating: │x 2 + 6x + 8│= x 2 + 6x + 8 №13.
Tenglamani yeching, javobingizdagi butun yechimlar sonini ko‘rsating: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14.
Javobingizda tenglamani yeching, tenglamaning ildizi bo'lmagan butun sonni ko'rsating: 
5-bo‘lim. │F(x)│= │G(x)│ ko‘rinishdagi tenglamalar
Tenglamaning ikkala tomoni manfiy bo'lmaganligi sababli, yechim ikkita holatni ko'rib chiqishni o'z ichiga oladi: submodulli ifodalar ishorada teng yoki qarama-qarshidir. Shuning uchun dastlabki tenglama ikkita tenglamaning birikmasiga ekvivalentdir: │ F(x)│= │ G(x)│
Misollar:
№1.
Tenglamani yeching, javobingizda butun ildizni ko'rsating: │x + 3│=│2x - 1│ 
Javob: butun ildiz x = 4.№2.
Tenglamani yeching: │
x – x 2 - 1│=│2x – 3 – x 2 │ 
Javob: x = 2.№3
.
Tenglamani yeching va javobingizda ildizlarning ko'paytmasini ko'rsating: 
Ildiz tenglamalari 4x 2 + 2x – 1 = 0 x 1.2 = - 1±√5 / 4 Javob: ildizlarning mahsuloti - 0,25. Mashqlar:
№15
. Tenglamani yeching va javobingizda butun yechimni ko'rsating: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16.
Tenglamani yeching, javobingizda kichikroq ildizni ko'rsating:│5x - 3│=│7 - x│ №17
. Tenglamani yeching va javobingizdagi ildizlar yig‘indisini ko‘rsating: 
6-bo'lim. Nostandart tenglamalarni yechishga misollar
Ushbu bo'limda biz nostandart tenglamalar misollarini ko'rib chiqamiz, ularni hal qilishda ifodaning mutlaq qiymati ta'rifi bilan ochiladi. Misollar:№1.
Tenglamani yeching, javobingizdagi ildizlar yig‘indisini ko‘rsating: x · │x│- 5x – 6 = 0 
Javob: ildizlarning yig'indisi 1 ga teng №2.
.
Tenglamani yeching, javobingizda kichikroq ildizni ko'rsating: x 2 - 4x · 
- 5 = 0 
Javob: kichikroq ildiz x = - 5. №3.
Tenglamani yeching: 
Javob: x = -1. Mashqlar:
№18.
Tenglamani yeching va ildizlar yig‘indisini ko‘rsating: x · │3x + 5│= 3x 2 + 4x + 3
№19.
Tenglamani yeching: x 2 – 3x = 
№20.
Tenglamani yeching: 
7-bo'lim. │F(x)│+│G(x)│=0 ko'rinishdagi tenglamalar
Ushbu turdagi tenglamaning chap tomonida manfiy bo'lmagan miqdorlarning yig'indisi joylashganligini payqash oson. Demak, asl tenglama bir vaqtning o‘zida ikkala hadi nolga teng bo‘lgandagina yechimga ega bo‘ladi. Tenglama tenglamalar tizimiga ekvivalent: │ F(x)│+│ G(x)│=0
Misollar:
№1
. Tenglamani yeching: 
Javob: x = 2. №2.
Tenglamani yeching: Javob: x = 1. Mashqlar:
№21.
Tenglamani yeching: №22
. Tenglamani yeching va javobingizdagi ildizlar yig‘indisini ko‘rsating: №23
. Tenglamani yeching va javobingizdagi yechimlar sonini ko'rsating: 8-bo‘lim. │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m ko‘rinishdagi tenglamalar
Ushbu turdagi tenglamalarni yechish uchun interval usuli qo'llaniladi. Agar biz uni modullarni ketma-ket kengaytirish orqali hal qilsak, biz olamiz n tizimlar to'plami, bu juda og'ir va noqulay. Intervalli usul algoritmini ko'rib chiqamiz: 1). O'zgaruvchan qiymatlarni toping X, buning uchun har bir modul nolga teng (submodulli ifodalarning nollari):
2). Topilgan qiymatlarni intervallarga bo'lingan raqam chizig'ida belgilang (oraliqlar soni mos ravishda teng n+1
) 3). Olingan oraliqlarning har birida har bir modul qaysi belgi bilan aniqlanishini aniqlang (yechimni ishlab chiqishda siz raqamlar chizig'idan foydalanishingiz mumkin, undagi belgilarni belgilashingiz mumkin) 4). Dastlabki tenglama agregatga teng n+1
tizimlar, ularning har birida o'zgaruvchining a'zoligi ko'rsatilgan X intervallardan biri. Misollar:
№1
. Tenglamani yeching va javobingizdagi eng katta ildizni ko'rsating: 
1). Submodulli ifodalarning nollarini topamiz: x = 2; x = -3 2). Keling, topilgan qiymatlarni raqamlar qatorida belgilaymiz va natijada olingan intervallarda har bir modul qanday belgi bilan aniqlanishini aniqlaymiz: x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- yechimlari yo'q tenglamaning ikkita ildizi bor. Javob: eng katta ildiz x = 2. №2.
Tenglamani yeching va javobingizda butun ildizni keltiring: 
1). Submodulli ifodalarning nollarini topamiz: x = 1,5; x = - 1 2). Topilgan qiymatlarni raqamlar qatorida belgilaymiz va hosil bo'lgan intervallarda har bir modul qanday belgi bilan aniqlanishini aniqlaymiz: x + 1 x + 1 x + 1 - + + -1 1,5 x 2x – 3 2x – 3 2x – 3 - - +
3).
Oxirgi tizimning yechimlari yo'q, shuning uchun tenglama ikkita ildizga ega. Tenglamani echishda siz ikkinchi modul oldidagi "-" belgisiga e'tibor berishingiz kerak. Javob: butun ildiz x = 7. №3.
Tenglamani yeching, javobingizdagi ildizlar yig'indisini ko'rsating: 1). Submodulli ifodalarning nollarini topamiz: x = 5; x = 1; x = - 2 2). Topilgan qiymatlarni raqamlar qatorida belgilaymiz va natijada har bir modul qanday belgi bilan ochilganligini aniqlaymiz: x – 5 x – 5 x – 5 x – 5 - - - + -2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
Tenglamaning ikkita ildizi bor x = 0 va 2. Javob: ildizlarning yig'indisi 2 ga teng. №4
.
Tenglamani yeching: 1). Submodulli ifodalarning nollarini topamiz: x = 1; x = 2; x = 3. 2). Olingan intervallarda har bir modul qanday belgi bilan ochilganligini aniqlaylik. 3). 
Keling, yechimlarni birlashtiraylik birinchi uchta tizimlari Javob: ; x = 5.Mashqlar: №24. Tenglamani yeching:
№25.
Tenglamani yeching va javobingizdagi ildizlar yig‘indisini ko‘rsating: №26.
Tenglamani yeching va javobingizda kichikroq ildizni ko'rsating: №27.
Tenglamani yeching va javobingizda kattaroq ildizni ko'rsating: 9-bo'lim. Bir nechta modullarni o'z ichiga olgan tenglamalar
Bir nechta modullarni o'z ichiga olgan tenglamalar submodulyar ifodalarda mutlaq qiymatlar mavjudligini taxmin qiladi. Ushbu turdagi tenglamalarni echishning asosiy printsipi "tashqi" dan boshlab modullarni ketma-ket ochishdir. Yechish vaqtida 1-sonli, 3-sonli bo'limlarda muhokama qilingan texnikalar qo'llaniladi.Misollar:
№1.
Tenglamani yeching: 
Javob: x = 1; - o'n bir. №2.
Tenglamani yeching:
Javob: x = 0; 4; - 4. №3.
Tenglamani yeching va javobingizda ildizlarning ko'paytmasini ko'rsating: 
Javob: ildizlarning hosilasi – 8 ga teng. №4.
Tenglamani yeching: 
Populyatsiya tenglamalarini belgilaylik (1)
Va (2)
va dizayn qulayligi uchun ularning har birining yechimini alohida ko'rib chiqing. Ikkala tenglama ham bir nechta modullarni o'z ichiga olganligi sababli, tizimlar to'plamiga ekvivalent o'tishni amalga oshirish qulayroqdir. (1)
(2)
Javob:
Mashqlar:
№36.
Tenglamani yeching, javobingizdagi ildizlar yig‘indisini ko‘rsating: 5 │3x-5│ = 25 x №37.
Tenglamani yeching, agar bir nechta ildiz bo'lsa, javobingizdagi ildizlar yig'indisini ko'rsating: │x + 2│ x – 3x – 10 = 1 №38.
Tenglamani yeching: 3 │2x -4│ = 9 │x│ №39.
Tenglamani yeching va javobingizdagi ildizlar sonini ko'rsating: 2 │ sin x│ = √2 №40
. Tenglamani yeching va javobingizdagi ildizlar sonini ko'rsating:
3-bo'lim. Logarifmik tenglamalar.
Quyidagi tenglamalarni yechishdan oldin logarifmlarning xossalari va logarifmik funktsiyani ko'rib chiqish kerak. Misollar: №1. Tenglamani yeching, javobingizdagi ildizlarning mahsulotini ko'rsating: log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 11-holat: agar x ≥ - 1 bo‘lsa, log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – x ≥ - 1 2 shartni qanoatlantiradi: agar x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – x - 1 shartni qanoatlantiradi
Javob: ildizlarning hosilasi - 15.
№2.
Tenglamani yeching, javobingizdagi ildizlar yig'indisini ko'rsating: lg 
O.D.Z. 
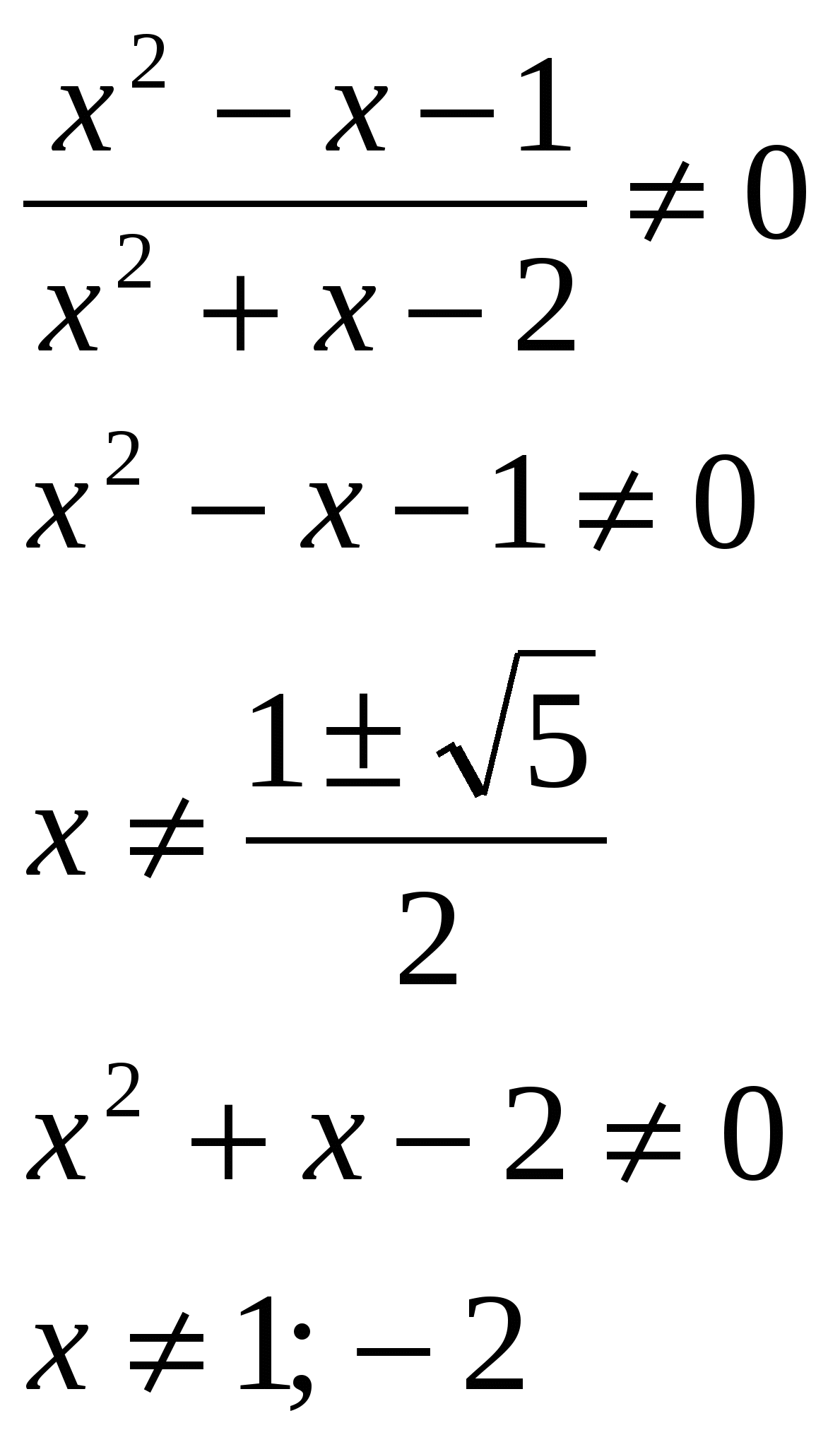
Javob: ildizlarning yig'indisi 0,5 ga teng.
№3.
Tenglamani yeching: log 5 
O.D.Z. 
Javob: x = 9. №4.
Tenglamani yeching: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Boshqa bazaga o'tish uchun formuladan foydalanamiz. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Submodulli ifodalarning nollarini topamiz: x = 25; x = Bu raqamlar qabul qilinadigan qiymatlar oralig'ini uchta intervalga ajratadi, shuning uchun tenglama uchta tizim to'plamiga teng. 
Javob:)
